题目内容
在 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求角
,求角 的大小及向量
的大小及向量 在
在 方向上的投影.
方向上的投影.
(1) ;(2)
;(2) ,向量
,向量 在
在 方向上的投影
方向上的投影
 .
.
解析试题分析:(1)由向量数量积坐标形式列式,可求得 的值,再利用平方关系可求得
的值,再利用平方关系可求得 的值;(2)先利用正弦定理可求得
的值;(2)先利用正弦定理可求得 的值,再利用大边对大角可求得角
的值,再利用大边对大角可求得角 的大小.由投影的定义可求得向量
的大小.由投影的定义可求得向量 在
在 方向上的投影.
方向上的投影.
试题解析:(1)由 ,得
,得 , 1分
, 1分
 , 2分
, 2分
 .
. 
 . 3分
. 3分 . 4分
. 4分
(2)由正弦定理,有 , 5分
, 5分
 . 6分
. 6分 ,
, , 7分
, 7分 . 8分
. 8分
由余弦定理,有 , 9分
, 9分 或
或 (舍去). 10分
(舍去). 10分
故向量 在
在 方向上的投影为
方向上的投影为 11分
11分 . 12分
. 12分
考点:1、向量数量积、投影;2、三角恒等变换;3、解三角形.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
在数列1,1,2,3,5,8, ,21,34,55,…中,
,21,34,55,…中, 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
已知数列 满足
满足 若
若 则
则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
 =(cos
=(cos ,cos(
,cos( ),
), =(
=( ,sin
,sin
 的值;
的值; ,求
,求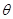 ;
; ,求证:
,求证: .
. =
= +λ·
+λ· (λ∈R),试问:
(λ∈R),试问: .
. ,求
,求 ;
; 的最大值.
的最大值. 是函数
是函数 ,
, )一个周期内图象上的两点,函数
)一个周期内图象上的两点,函数 的图象与
的图象与 轴交于点
轴交于点 ,满足
,满足 .
. 在区间
在区间 内的零点.
内的零点. ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
. 的值;
的值; 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 上的最大值和最小值.
上的最大值和最小值. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.