题目内容
数列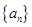 满足
满足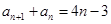
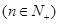 。
。
(Ⅰ)若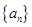 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若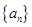 满足
满足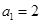 ,
, 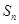 为
为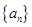 的前
的前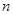 项和,求
项和,求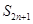 。
。
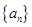 满足
满足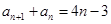
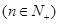 。
。(Ⅰ)若
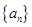 是等差数列,求其通项公式;
是等差数列,求其通项公式;(Ⅱ)若
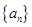 满足
满足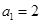 ,
, 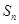 为
为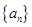 的前
的前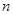 项和,求
项和,求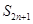 。
。(1) (2)
(2)
 (2)
(2)
试题分析:解:(I)由题意得
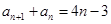 …①
…①  …②.
…②.②-①得
 ,∵{
,∵{ }是等差数列,设公差为d,∴d=2, 4分
}是等差数列,设公差为d,∴d=2, 4分∵
 ∴
∴ ,∴
,∴  ,∴
,∴ 7分
7分(Ⅱ)∵

 ,∴
,∴ 8分
8分又∵
 ,∴数列的奇数项与偶数项分别成等差数列,公差均为4
,∴数列的奇数项与偶数项分别成等差数列,公差均为4∴
 ,
, 11分
11分
=
 =
= 14分
14分点评:解决的关键是根据等差数列的通项公式以及分组求和 方法得到,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
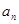 }满足
}满足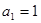 ,且
,且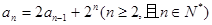
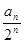 }是等差数列;
}是等差数列;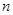 项之和
项之和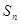 ,求证:
,求证: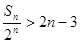 .
.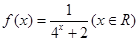 .
.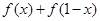 的值;
的值;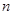 项和公式的推导方法,求:
项和公式的推导方法,求: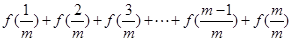 的值.
的值.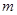 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为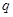 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )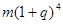 元
元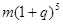 元
元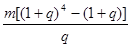 元
元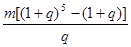 元
元
 行的第m个数为
行的第m个数为
 .
.
 ,
,
 ,
,
 值的大小;
值的大小;
 的关系式,并求出
的关系式,并求出 的前
的前 项和为
项和为 ,则数列
,则数列 的前100项和为
的前100项和为



 中,
中, ;设数列
;设数列 的前
的前 项和为
项和为 ,则
,则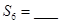
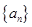 的前
的前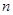 项和为
项和为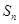 ,
,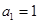 ,
,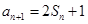
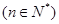 ,等差数列
,等差数列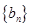 满足
满足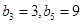 .
.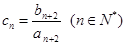 ,求证
,求证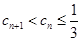 .
.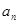 }中,
}中,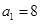 ,
,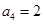 ,且满足
,且满足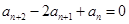
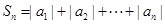 ,求
,求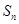 .
.