题目内容
9.已知正方体ABCD-A1B1C1D1的各顶点都在球O表面上,在球O内任取一点M,则点M在正方体ABCD-A1B1C1D1内的概率是( )| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{3\sqrt{2}}{2π}$ | C. | $\frac{\sqrt{3}}{3π}$ | D. | $\frac{2\sqrt{3}}{3π}$ |
分析 设正方体的棱长为a,则外接球的半径为$\frac{\sqrt{3}}{2}$a,以面积为测度,即可求出在球O内任取一点M,则点M在正方体ABCD-A1B1C1D1内的概率.
解答 解:设正方体的棱长为a,则外接球的半径为$\frac{\sqrt{3}}{2}$a,
∴在球O内任取一点M,则点M在正方体ABCD-A1B1C1D1内的概率是$\frac{{a}^{3}}{\frac{4}{3}π•(\frac{\sqrt{3}}{2}a)^{3}}$=$\frac{2\sqrt{3}}{3π}$,
故选:D.
点评 本题考查几何概型,考查学生的计算能力,正确求面积是关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
20.下列选项中说法错误的是( )
| A. | 27是3的倍数或27是9的倍数 | |
| B. | 平行四边形的对角线互相垂直且平分 | |
| C. | 平行四边形的对角线互相垂直或平分 | |
| D. | 1是方程x-1=0的根,且是方程x2-5x+4=0的根 |
4.设等差数列{an}满足sina4cosa7-cosa4sina7=1,公差d∈(-1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
| A. | $(\frac{7π}{6},\frac{4π}{3})$ | B. | $[{\frac{7π}{6},\frac{4π}{3}}]$ | C. | $(\frac{4π}{3},\frac{3π}{2})$ | D. | $[{\frac{4π}{3},\frac{3π}{2}}]$ |
18.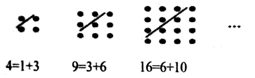 古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
 古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )
古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( )| A. | 16=3+13 | B. | 25=9+16 | C. | 36=10+26 | D. | 49=21+28 |
19.对[25,55]岁的人群随机抽取n人进行了生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
(Ⅰ)补全频率分布直方图并求n、a、p的值;
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.