题目内容
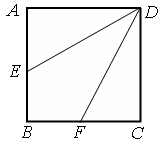
如图,边长为2的正方形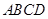 中,点
中,点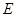 是
是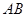 的中点,点
的中点,点 是
是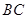 的中点,将△
的中点,将△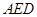 、△
、△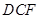 分别沿
分别沿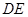 、
、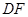 折起,使
折起,使 、
、 两点重合于点
两点重合于点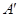 ,连接
,连接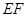 ,
,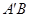 .
.
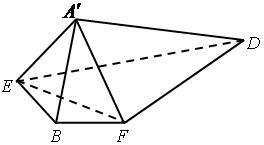
(1)求证: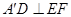 ;
;
(2)求二面角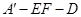 的余弦值.
的余弦值.
(1)详见解析;(2)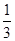 .
.
解析试题分析:(1)由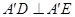 ,
,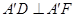 证出
证出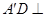 平面
平面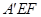 ,进而证出结论;(2)方法一:根据对称可判断
,进而证出结论;(2)方法一:根据对称可判断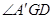 即为所求,由(1)可证△
即为所求,由(1)可证△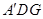 为直角三角形,再求出边长即可;方法二:建系,求出平面
为直角三角形,再求出边长即可;方法二:建系,求出平面 和平面
和平面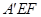 的法向量,两法向量的夹角的余弦值即为所求.
的法向量,两法向量的夹角的余弦值即为所求.
试题解析:(1)在正方形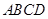 中,有
中,有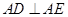 ,
,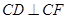 1分
1分
则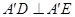 ,
,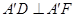 2分
2分
又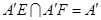 3分
3分
∴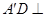 平面
平面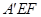 4分
4分
而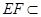 平面
平面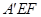 ,∴
,∴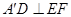 5分
5分
(2)方法一:连接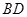 交
交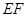 于点
于点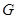 ,连接
,连接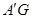 6分
6分
∵在正方形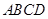 中,点
中,点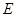 是
是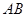 的中点,点
的中点,点 是
是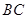 的中点,
的中点,
∴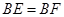 ,
,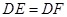 ,
,
∴点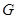 为
为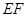 的中点,
的中点,
且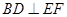 7分
7分
∵正方形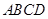 的边长为2,∴
的边长为2,∴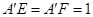 ,∴
,∴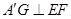 8分
8分
∴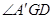 为二面角
为二面角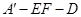 的平面角 9分
的平面角 9分
由(1)可得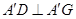 ,
,
∴△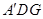 为直角三角形 10分
为直角三角形 10分
∵正方形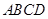 的边长为2,
的边长为2,
∴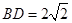 ,
,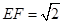 ,
,
∴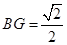 ,
,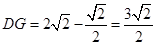 ,
,
又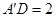 11分
11分
∴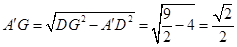

练习册系列答案
相关题目
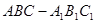 ,底面
,底面 中
中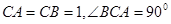 ,棱
,棱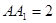 ,
,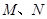 分别为
分别为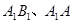 的中点.
的中点.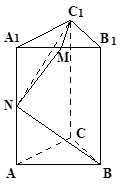
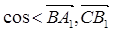 >的值;
>的值;
 ,E,F分别是AB,AP的中点.
,E,F分别是AB,AP的中点.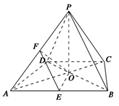
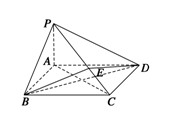
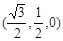 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.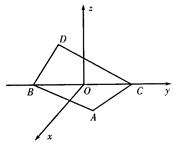
 的值.
的值.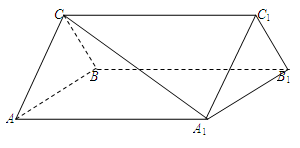
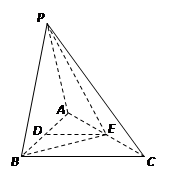
 ,使得平面
,使得平面
 平面ABD;
平面ABD;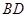 与平面
与平面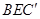 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值. 的长方体被截面
的长方体被截面 所截面而得到的,其中
所截面而得到的,其中 .
. 的长;
的长;