题目内容
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.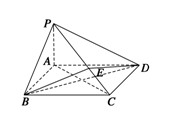
(1) 证明:BD⊥平面PAC;
(2) 若PA=1,AD=2,求二面角B-PC-A的正切值.
(1)见解析;(2)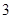 .
.
解析试题分析:(1)先利用直线与平面垂直的性质定理,得到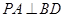 和
和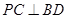 ,因为
,因为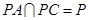 ,所以利用直线与平面垂直的判定定理可知,
,所以利用直线与平面垂直的判定定理可知,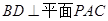 ;(2)首先分别以射线
;(2)首先分别以射线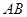 ,
,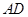 ,
,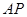 为
为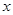 轴,
轴,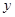 轴,
轴,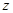 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系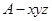 ,由直线与平面垂直的性质定理得到
,由直线与平面垂直的性质定理得到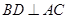 ,那么矩形
,那么矩形 为正方形,由此可知此正方形的边的长度,根据坐标系表示四棱锥出各个顶点的坐标,分别求出平面
为正方形,由此可知此正方形的边的长度,根据坐标系表示四棱锥出各个顶点的坐标,分别求出平面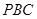 和平面
和平面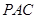 的法向量的坐标,根据二面角与其法向量夹角的关系,求得二面角的余弦值,再由同角三角函数的基本关系得到所求二面角的正切值.
的法向量的坐标,根据二面角与其法向量夹角的关系,求得二面角的余弦值,再由同角三角函数的基本关系得到所求二面角的正切值.
试题解析:(1)证明 ∵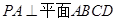 ,
,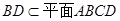 ,∴
,∴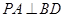 .2分
.2分
同理由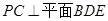 ,可证得
,可证得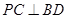 .
.
又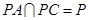 ,∴
,∴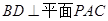 . 4分
. 4分
(2)如图,分别以射线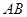 ,
,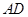 ,
,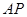 为
为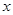 轴,
轴,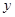 轴,
轴,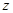 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系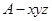 .
.
由(1)知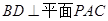 ,又
,又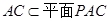 , ∴
, ∴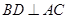 .
.
故矩形 为正方形,∴
为正方形,∴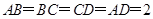 . 6分
. 6分
∴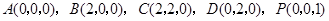 .
.
∴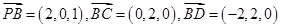 .
.
设平面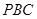 的一个法向量为
的一个法向量为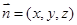 ,则
,则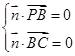 ,即
,即 ,
,
∴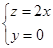 ,取
,取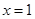 ,得
,得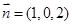 .
.
∵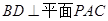 ,∴
,∴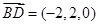 为平面
为平面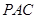 的一个法向量.10分
的一个法向量.10分
所以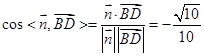 . 11分
. 11分
设二面角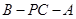 的平面角为
的平面角为 ,由图知
,由图知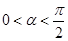 ,
,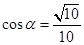 ,所以
,所以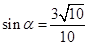 .
.
∴ 所以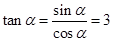 ,即二面角
,即二面角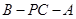 的正切值为
的正切值为 . 12分
. 12分
考点:1.直线与平面垂直的判定定理;2.直线与平面垂直的性质定理;3.平面和平面所成的角(二面角);4.勾股定理;5.同角三角函数的基本关系;6.平面的法向量

练习册系列答案
相关题目
 .
.
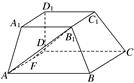
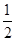 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).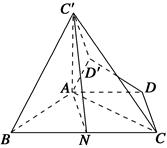
 ,求AB的长.
,求AB的长.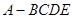 中,
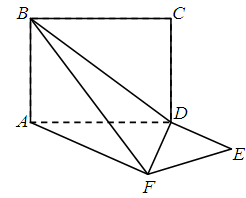
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
, .
.
 是
是 的中点,求证:
的中点,求证: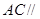 平面
平面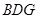 ;
;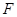 在线段
在线段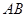 上什么位置时,二面角
上什么位置时,二面角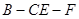 的余弦值为
的余弦值为 .
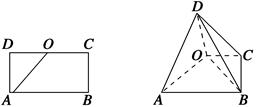
.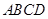 中,点
中,点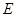 是
是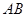 的中点,点
的中点,点 是
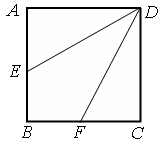
是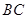 的中点,将△
的中点,将△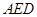 、△
、△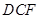 分别沿
分别沿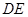 、
、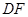 折起,使
折起,使 、
、 两点重合于点
两点重合于点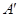 ,连接
,连接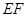 ,
,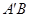 .
.
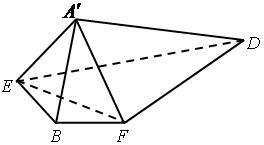
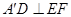 ;
;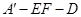 的余弦值.
的余弦值.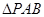 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,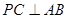 ,E为PD点上一点,满足
,E为PD点上一点,满足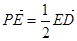
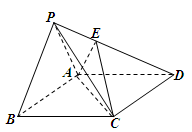
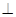 平面ABCD;
平面ABCD;