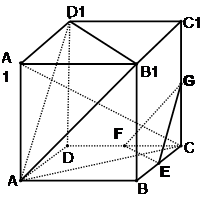题目内容
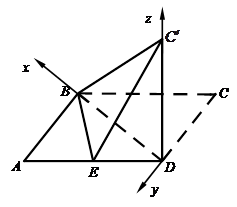
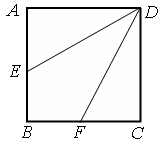
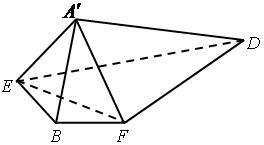
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△ ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.
(Ⅰ)求证: 平面ABD;
平面ABD;
(Ⅱ)求直线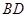 与平面
与平面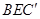 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(Ⅰ)先证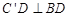 (Ⅱ)
(Ⅱ)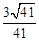 (Ⅲ)
(Ⅲ)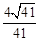
解析试题分析:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,
沿直线BD将△BCD翻折成△
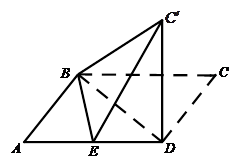
可知CD=6,BC’=BC=10,BD=8,
即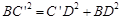 ,
,
故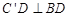 .
.
∵平面 ⊥平面
⊥平面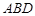 ,平面
,平面
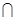 平面
平面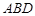 =
= ,
,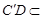 平面
平面 ,
,
∴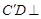 平面
平面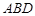 .
.
(Ⅱ)由(Ⅰ)知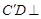 平面ABD,且
平面ABD,且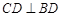 ,
,
如图,以D为原点,建立空间直角坐标系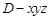 .
. 
则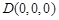 ,
,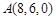 ,
, ,
,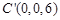 .
.
∵E是线段AD的中点,
∴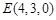 ,
,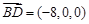 .
.
在平面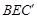 中,
中,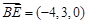 ,
,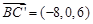 ,
,
设平面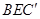 法向量为
法向量为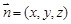 ,
,
∴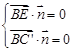 ,即
,即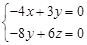 ,
,
令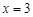 ,得
,得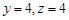 ,故
,故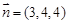 .
.
设直线 与平面
与平面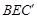 所成角为
所成角为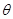 ,则
,则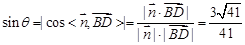 .
.
∴直线 与平面
与平面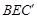 所成角的正弦值为
所成角的正弦值为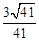 .
.
(Ⅲ)由(Ⅱ)知平面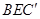 的法向量为
的法向量为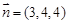 ,
,
而平面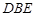 的法向量为
的法向量为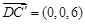 ,
,
∴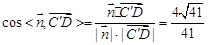 ,
,
因为二面角 为锐角,
为锐角,
所以二面角 的余弦值为
的余弦值为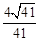 .
.
考点:用空间向量求平面间的夹角;直线与平面垂直的判定.
点评:本题重点考查线面垂直、线面角与二面角的平面角,以及翻折问题,学生必须要掌握在翻折的过程中,哪些是不变的,哪些是改变,这也是解决此类问题的关键.

练习册系列答案
相关题目
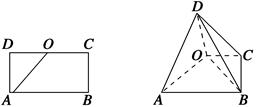
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B.1+ | C. | D.1+ |
 .
.
 中,点
中,点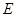 是
是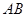 的中点,点
的中点,点 是
是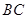 的中点,将△
的中点,将△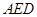 、△
、△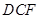 分别沿
分别沿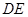 、
、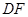 折起,使
折起,使 、
、 两点重合于点
两点重合于点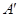 ,连接
,连接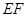 ,
, .
.
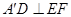 ;
;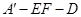 的余弦值.
的余弦值.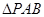 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,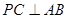 ,E为PD点上一点,满足
,E为PD点上一点,满足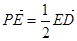
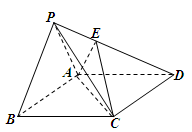
 平面ABCD;
平面ABCD; 的正方体
的正方体 中,
中, 、
、 分别是
分别是 、
、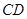 的中点,试用向量的方法:
的中点,试用向量的方法: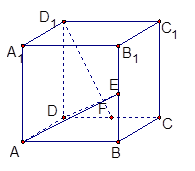
 求证:
求证: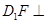 平面
平面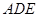 ;
; 求
求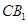 与平面
与平面
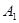 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;