题目内容
在如图所示的空间直角坐标系O-xyz中,原点O是BC的中点,A点坐标为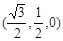 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.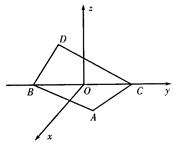
(Ⅰ)求D点坐标;
(Ⅱ)求 的值.
的值.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)D在平面yoz上,可知横坐标为0,再由 过D点作DH⊥BC,垂足为H.可知中坐标为OH,竖坐标为DH.
过D点作DH⊥BC,垂足为H.可知中坐标为OH,竖坐标为DH.
(Ⅱ)由向量 的数量积可得
的数量积可得 .
.
试题解析:(Ⅰ)在平面yoz上,过D点作DH⊥BC,垂足为H.
在△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,
得 ,
,


(Ⅱ)由 得
得
由题设知:B(0,-1,0),C(0,1,0),

 ,
, ,
,


考点:1、空间向量的坐标;2、向量的数量积 及向量数量积的夹角公式.
及向量数量积的夹角公式.

练习册系列答案
相关题目
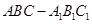 中,△ABC是正三角形,
中,△ABC是正三角形,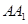
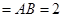 ,平面
,平面 平面
平面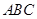 ,
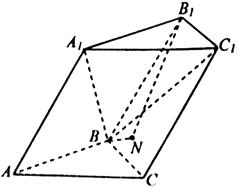
,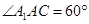 .
.
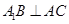 ;
;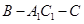 的余弦值;
的余弦值;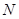 是平面
是平面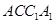 内的动点,求
内的动点,求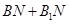 的最小值.
的最小值.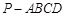 的底面
的底面 是直角梯形,
是直角梯形,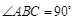 ,
,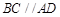 ,且
,且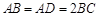 ,顶点
,顶点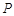 在底面
在底面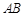 的中点
的中点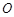 上.
上.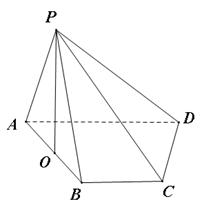
 ;
;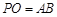 ,求直线
,求直线 与
与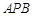 与平面
与平面 所成的二面角为
所成的二面角为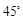 ,求
,求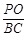 的值.
的值.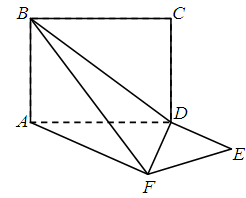
 ,求AB的长.
,求AB的长. 的所有棱长都为4,D为的
的所有棱长都为4,D为的 中点.
中点.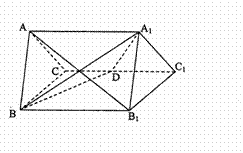
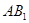 ⊥平面
⊥平面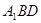 ;
;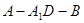 余弦值.
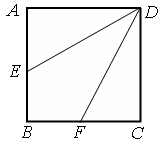
余弦值.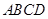 中,点
中,点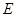 是
是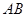 的中点,点
的中点,点 是
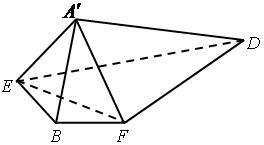
是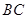 的中点,将△
的中点,将△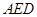 、△
、△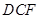 分别沿
分别沿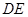 、
、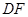 折起,使
折起,使 、
、 两点重合于点
两点重合于点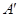 ,连接
,连接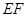 ,
,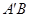 .
.
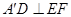 ;
;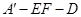 的余弦值.
的余弦值.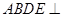 平面
平面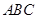 ,
,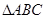 是等腰直角三角形,
是等腰直角三角形,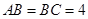 ,四边形
,四边形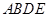 是直角梯形,
是直角梯形,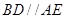 ,
,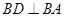 ,
,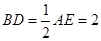 ,点
,点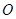 、
、 分别为
分别为 、
、 的中点.
的中点.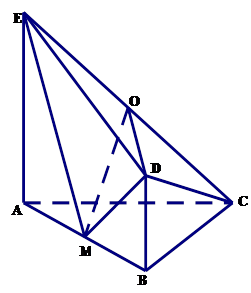
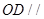 平面
平面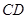 和平面
和平面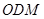 所成角的正弦值;
所成角的正弦值;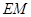 上找到一点
上找到一点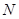 ,使得
,使得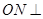 平面
平面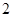 的正方体
的正方体 中,
中, 、
、 分别是
分别是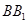 、
、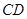 的中点,试用向量的方法:
的中点,试用向量的方法: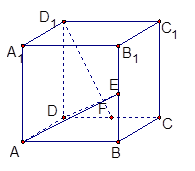
 求证:
求证: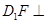 平面
平面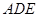 ;
; 求
求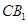 与平面
与平面