题目内容
18.( I)求值:log23•log34-log20.125-$\sqrt{2{7}^{\frac{2}{3}}}$;( II)求值:sin15°+cos15°.
分析 (Ⅰ)根据对数和指数幂的运算性质计算即可,
(Ⅱ)根据两角和的正弦公式计算即可.
解答 解:( I)原式=$\frac{lg3}{lg2}•\frac{lg4}{lg3}-{log_2}\frac{1}{8}-{27^{\frac{1}{3}}}=2-{log_2}{2^{-3}}-3=2+3-3=2$,
( II)原式=$\sqrt{2}$($\frac{\sqrt{2}}{2}$sin15°+$\frac{\sqrt{2}}{2}$cos15°)=$\sqrt{2}$sin60°=$\frac{\sqrt{6}}{2}$
点评 本题考查了对数的化简和三角函数的化简,属于基础题.

练习册系列答案
相关题目
12.已知P为抛物线y2=8x上一点,F为该抛物线焦点,若A点坐标为(3,2),则|PA|+|PF|最小值为( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 7 | D. | 11 |
6.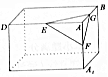 如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
 如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )
如图,用小刀切一块长方体橡皮的一个角,在棱AD、AA1、AB上的截点分别是E、F、G,则截面△EFG( )| A. | 一定是等边三角形 | B. | 一定是钝角三角形 | ||
| C. | 一定是锐角三角形 | D. | 一定是直角三角形 |
3.设函数f(x)=$\frac{{e}^{2}{x}^{2}+1}{x}$,g(x)=$\frac{{e}^{2}x}{{e}^{x}}$,对任意${x_1},{x_2}∈({\frac{1}{e},+∞})$,不等式$\frac{{g({x_1})}}{k}<\frac{{f({x_2})}}{k+2}$恒成立,则正数k的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |