题目内容

19．已知三棱柱ABC-A1B1C1的侧棱与底面垂直，体积为$\frac{9}{4}$，底面是边长为$\sqrt{3}$的正三角形．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（　　）
A．120°B．60°C．45°D．30°

分析 利用三棱柱ABC-A1B1C1的侧棱与底面垂直和线面角的定义可知，∠APA1为PA与平面A1B1C1所成角．利用三棱锥的体积计算公式可得AA1，再利用正三角形的性质可得A1P，在Rt△AA1P中，利用tan∠APA1=$\sqrt{3}$，可得结论．

解答 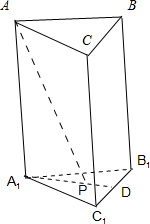解：如图所示，
∵AA1⊥底面A1B1C1，∴∠APA1为PA与平面A1B1C1所成角，
∵平面ABC∥平面A1B1C1，∴∠APA1为PA与平面ABC所成角．
∵${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{\sqrt{3}}{4}×3$=$\frac{3\sqrt{3}}{4}$．
∴V三棱柱ABC-A1B1C1=$\frac{3\sqrt{3}}{4}$AA1，解得AA1=$\sqrt{3}$．
又P为底面正三角形A1B1C1的中心，∴A1P=$\frac{2}{3}{A}_{1}D$=1，
在Rt△AA1P中，tan∠APA1=$\sqrt{3}$，
∴∠APA1=60°．
故选B．

点评 本题考查线面角，掌握正三角形的性质、线面角的定义是解题的关键．

练习册系列答案
相关题目
14．双曲线$\frac{x^2}{3}-\frac{y^2}{6}=1$的离心率e=（　　）
A．$\sqrt{3}$B．$\sqrt{2}$C．3D．$\sqrt{6}$
15．已知下列命题（其中a，b为直线，α为平面）：
①若一条直线垂直于平面内无数条直线，则这条直线与这个平面垂直；
②若一条直线平行于一个平面，则垂直于这条直线的直线一定垂直于这个平面；
③若a∥α，b⊥α，则a⊥b；
④若a⊥b，则过b有惟一α与a垂直．
上述四个命题中，是真命题的有③④．（填序号）
7．等差数列{an}中，2a1+3a2=11，2a3=a2+a6-4，其前n项和为Sn．
（1）求数列{an}的通项公式；
（2）设数列{bn}满足${b_n}=\frac{1}{{{S_{n+1}}-1}}$，求其前n项和Tn．
14．设直线l与平面α相交但不垂直，则下列命题错误的是（　　）
A．在平面α内存在直线a与直线l平行B．在平面α内存在直线a与直线l垂直
C．在平面α内存在直线a与直线l相交D．在平面α内存在直线a与直线l异面
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）的焦距为2，过短轴的一个端点与两个焦点的圆的面积为$\frac{4}{3}$π，过椭圆C的右焦点作斜率为k（k≠0）的直线l与椭圆C相交于A、B两点，线段AB的中点为P．
（1）求椭圆C的标准方程；
（2）过点P垂直于AB的直线与x轴交于点D，且|DP|=$\frac{3\sqrt{2}}{7}$，求k的值．
11．已知曲线C：$\left\{\begin{array}{l}{x=3\sqrt{3}cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$（θ为参数），直线l：ρ（cosθ-$\sqrt{3}$sinθ）=12．
（Ⅰ）求直线l的直角坐标方程及曲线C的普通方程；
（Ⅱ）设点P在曲线C上，求点P到直线l的距离的最小值．
8．已知直线l：x-y-1=0，以原点O为极点，x轴非负半轴为极轴，取相同长度单位建立极坐标系，曲线C的极坐标方程为ρ2-4ρsinθ=5．
（Ⅰ）将直线l写成参数方程$\left\{{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}}\right.$（t为参数，α∈[0，π））的形式，并求曲线C的直角坐标方程；
（Ⅱ）设直线l与曲线C交于点A，B（点A在第一象限）两点，若点M的直角坐标为（1，0），求△OMA的面积．
9．函数f（x）=x2-2ax-2alnx（a∈R），则下列说法不正确的命题个数是（　　）
①当a＜0时，函数y=f（x）有零点；
②若函数y=f（x）有零点，则a＜0；
③存在a＞0，函数y=f（x）有唯一的零点；
④若a≤1，则函数y=f（x）有唯一的零点．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网