题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系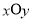 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(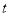 为参数),以原点
为参数),以原点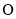 为极点,以
为极点,以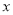 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线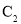 的极坐标方程为
的极坐标方程为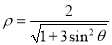 .
.
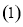 求曲线
求曲线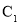 的普通方程与曲线
的普通方程与曲线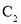 的直角坐标方程;
的直角坐标方程;
 试判断曲线
试判断曲线 与
与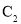 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
(1)曲线 :
: ,曲线
,曲线 :
: ;(2)
;(2)  .
.
【解析】
试题分析:(1) 根据参数方程与普通方程的关系,对于曲线 消去参数可得:
消去参数可得: ,再根据极坐标方程与直角坐标方程的关系,对于曲线
,再根据极坐标方程与直角坐标方程的关系,对于曲线 可转化为:
可转化为: ;(2) 根据题意显然曲线
;(2) 根据题意显然曲线 :
: 为直线,则其参数方程可写为
为直线,则其参数方程可写为 (为参数)与曲线
(为参数)与曲线 :
: 联立,可知
联立,可知 ,所以
,所以 与
与 存在两个交点,由
存在两个交点,由 ,
, ,得
,得 .
.
试题解析:(1) 对于曲线 有
有 ,对于曲线
,对于曲线 有
有 .(5分)
.(5分)
(2) 显然曲线 :
: 为直线,则其参数方程可写为
为直线,则其参数方程可写为 (为参数)与曲线
(为参数)与曲线 :
: 联立,可知
联立,可知 ,所以
,所以 与
与 存在两个交点,
存在两个交点,
由 ,
, ,得
,得 . (10分)
. (10分)
考点:1.极坐标方程与平面直角坐标方程的互化;2.利用直线的参数方程的几何意义求解

练习册系列答案
相关题目
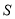 的值为( )
的值为( )
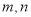 是两条不同直线,
是两条不同直线,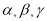 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )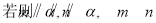
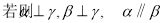
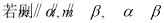
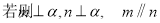
 = _________.
= _________. 的图像,只需要将函数
的图像,只需要将函数 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
 已知
已知 、
、 、
、 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
, 的值;
的值; 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率.
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率. 的前
的前 项和为
项和为 ,且
,且 ,
, 为常数列,则
为常数列,则 ( )
( ) B.
B. C.
C. D.
D.
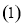 已知
已知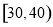 、
、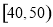 、
、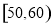 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
,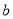 的值;
的值;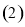 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和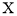 的分布列与数学期望.
的分布列与数学期望.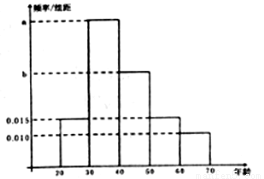
 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是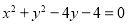 ,双曲线的左、右顶点
,双曲线的左、右顶点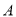 、
、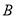 是该圆与
是该圆与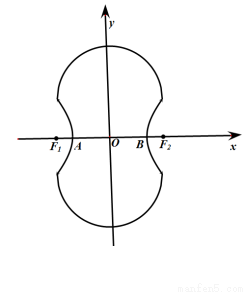
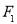 、
、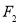 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点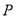 ,使得
,使得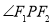 是直角.
是直角.