题目内容
(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.

 已知
已知 、
、 、
、 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求 ,
, 的值;
的值;
 该电子商务平台将年龄在
该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率.
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,并在这5人中随机抽取3人进行回访,求此三人获得代金券总和为200元的概率.
(1)  ,
, .(2)
.(2) 
【解析】
试题分析:(1)根据频率直方图中结论:所有频率之和为1,则有: ,即有:
,即有: ,又由条件:
,又由条件: 、
、 、
、 三个年龄段的上网购物者人数成等差数列,则有:
三个年龄段的上网购物者人数成等差数列,则有: ,解方程组得:
,解方程组得: ,
, ;(2) 根据(1)中:
;(2) 根据(1)中: ,可得高消费人群所占比例为
,可得高消费人群所占比例为 ,有利用分层抽样从样本中抽取5人,其中属于高消费人群的为3人,属于潜在消费人群的为2人. 由古典概率模型的求法:令高消费的人为
,有利用分层抽样从样本中抽取5人,其中属于高消费人群的为3人,属于潜在消费人群的为2人. 由古典概率模型的求法:令高消费的人为 ,潜在消费的人为
,潜在消费的人为 ,从中取出三人,例举总共有:
,从中取出三人,例举总共有: 这10种情况,其中
这10种情况,其中

 为获得代金卷总和为200元的情况,运用概率公式可求出三人获得代金券总和为200元的概率.
为获得代金卷总和为200元的情况,运用概率公式可求出三人获得代金券总和为200元的概率.
试题解析:(1)由图可知 ,
, . (4分)
. (4分)
利用分层抽样从样本中抽取5人,其中属于高消费人群的为3人,
属于潜在消费人群的为2人. (6分)
令高消费的人为 ,潜在消费的人为
,潜在消费的人为 ,从中取出三人,
,从中取出三人,
总共有: 10种情况,(8分)
10种情况,(8分)
其中 为获得代金卷总和为200元的情况,(10分)
为获得代金卷总和为200元的情况,(10分)
因此,三人获得代金券总和为200元的概率为 . (12分)
. (12分)
考点:考查统计与概率的相关知识

练习册系列答案
相关题目
 ( )
( ) B.
B. C.
C. D.
D.
 的零点所在的区间为( )
的零点所在的区间为( ) B.
B. C.
C. D.
D.
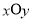 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(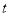 为参数),以原点
为参数),以原点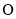 为极点,以
为极点,以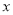 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线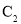 的极坐标方程为
的极坐标方程为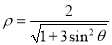 .
.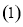 求曲线
求曲线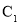 的普通方程与曲线
的普通方程与曲线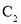 的直角坐标方程;
的直角坐标方程; 试判断曲线
试判断曲线 与
与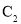 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由. ,则
,则 .
.
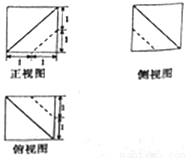
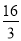 B.
B.
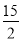 D.
D.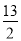
 的展开式中常数项为 .
的展开式中常数项为 .
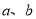 是两条不同的直线,
是两条不同的直线,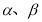 是两个不同的平面,则下面四个命题中错误的是( ).
是两个不同的平面,则下面四个命题中错误的是( ).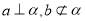 ,则
,则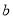 //
//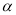
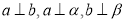 ,则
,则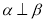
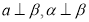 ,则
,则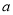 //
//
 //
// ,则
,则