题目内容
(本题满分14分)本题共2小题,第(1)小题6分,第(2)小题8分.
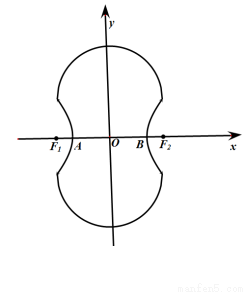
如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是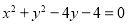 ,双曲线的左、右顶点
,双曲线的左、右顶点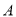 、
、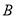 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为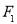 、
、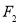 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点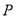 ,使得
,使得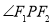 是直角.
是直角.
(1)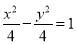 ,(2)满足条件的点有4个,分别为
,(2)满足条件的点有4个,分别为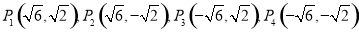 .
.
【解析】
试题分析: 由于上半个圆所在圆方程是 ,令
,令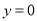 ,求出
,求出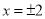 ,得双曲线的顶点,可知
,得双曲线的顶点,可知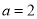 ,又双曲线与半圆相交于与
,又双曲线与半圆相交于与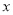 轴平行的直径的两端点,令
轴平行的直径的两端点,令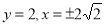 ,双曲线过点
,双曲线过点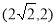 ,满足双曲线方程,待定系数法求出双曲线方程;第二步由于点
,满足双曲线方程,待定系数法求出双曲线方程;第二步由于点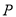 满足
满足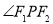 是直角,则点
是直角,则点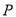 在以
在以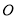 为圆心半径为
为圆心半径为 的圆上,满足
的圆上,满足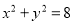 ,把圆的方程与双曲线方程联立解出交点坐标,由于
,把圆的方程与双曲线方程联立解出交点坐标,由于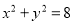 与上下两圆弧无交点,所以交点只有求出的四个 .
与上下两圆弧无交点,所以交点只有求出的四个 .
试题解析:(1)设双曲线的方程为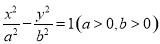 ,在已知圆的方程中,令
,在已知圆的方程中,令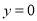 ,
,
得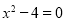 ,即
,即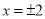 ,则双曲线的左、右顶点为
,则双曲线的左、右顶点为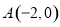 、
、 ,于是
,于是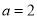 ,令
,令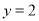 ,可得
,可得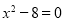 ,解得
,解得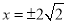 ,即双曲线过点
,即双曲线过点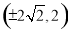 ,则
,则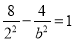 所以
所以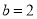 ,
,
所以所求双曲线方程为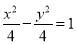 .
.
(2)由(1)得双曲线的两个焦点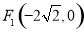 ,
,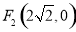 ,当
,当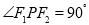 时,设点
时,设点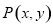 ,
,
①若点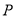 在双曲线上,得
在双曲线上,得 ,由
,由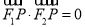 ,有
,有 则
则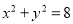 ,
,
由 ,解得
,解得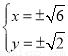 所以
所以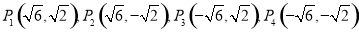
②若点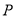 在上半圆上,则
在上半圆上,则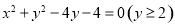 ,由
,由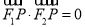 ,得
,得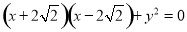 ,
,
由 无解.
无解.
综上,满足条件的点有4个,分别为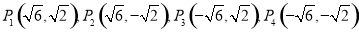 .
.
考点:1.求双曲线方程;2.求曲线的交点;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
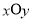 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(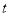 为参数),以原点
为参数),以原点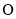 为极点,以
为极点,以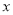 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线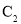 的极坐标方程为
的极坐标方程为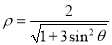 .
.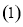 求曲线
求曲线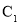 的普通方程与曲线
的普通方程与曲线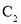 的直角坐标方程;
的直角坐标方程; 试判断曲线
试判断曲线 与
与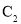 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.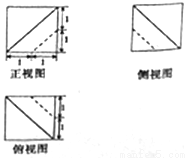
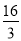 B.
B.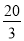
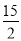 D.
D.
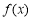 满足
满足 ,当
,当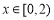 时,
时, 函数
函数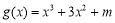 .若
.若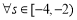 ,
,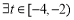 ,不等式
,不等式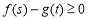 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )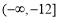 (B)
(B)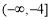
 (D)
(D)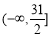
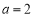 ”是“直线
”是“直线 和
和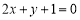 互相平行”的 ( )
互相平行”的 ( )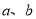 是两条不同的直线,
是两条不同的直线,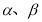 是两个不同的平面,则下面四个命题中错误的是( ).
是两个不同的平面,则下面四个命题中错误的是( ).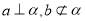 ,则
,则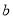 //
//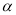
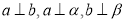 ,则
,则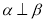
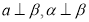 ,则
,则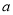 //
//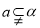
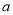 //
// ,则
,则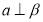
 的动弦
的动弦 的长为
的长为 ,则弦
,则弦 到
到 轴的最短距离是 .
轴的最短距离是 .  分别为双曲线
分别为双曲线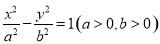 的左,右焦点,P为双曲线右支上的一点,且
的左,右焦点,P为双曲线右支上的一点,且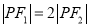 .若
.若 为等腰三角形,则该双曲线的离心率为_________.
为等腰三角形,则该双曲线的离心率为_________. 的零点所在的大致区间是
的零点所在的大致区间是 B.
B.  C.
C.  D.
D. 