题目内容
【题目】已知向量![]() ,
,![]() ,且函数
,且函数![]() .若函数
.若函数![]() 的图象上两个相邻的对称轴距离为
的图象上两个相邻的对称轴距离为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若方程![]() 在
在![]() 时,有两个不同实数根
时,有两个不同实数根![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的值;
的值;
(Ⅲ)若函数![]() 在
在![]() 的最大值为2,求实数
的最大值为2,求实数![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]()
【解析】
(Ⅰ)根据三角恒等变换公式化简![]() ,根据周期计算
,根据周期计算![]() ,从而得出
,从而得出![]() 的解析式;(Ⅱ)求出
的解析式;(Ⅱ)求出![]() 在
在![]() ,
,![]() 上的单调性,计算最值和区间端点函数值,从而得出
上的单调性,计算最值和区间端点函数值,从而得出![]() 的范围,根据对称性得出
的范围,根据对称性得出![]() 的值;(Ⅲ)令
的值;(Ⅲ)令![]() ,求出
,求出![]() 的范围和
的范围和![]() 关于
关于![]() 的二次函数,讨论二次函数单调性,根据最大值列方程求出
的二次函数,讨论二次函数单调性,根据最大值列方程求出![]() 的值.
的值.
(Ⅰ)∵![]() ,
,![]() ,
,
∴![]()
![]()
若函数![]() 的图象上两个相邻的对称轴距离为
的图象上两个相邻的对称轴距离为![]() ,
,
则函数![]() 的周期
的周期![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
(Ⅱ)由(Ⅰ)知,![]() ,
,
当![]() 时,
时,![]()
∴若方程![]() 在
在![]() 有两个不同实数根,则
有两个不同实数根,则![]() .
.
∴令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴函数在![]() 内的对称轴为
内的对称轴为![]() ,
,
∵![]() ,
,![]() 是方程
是方程![]() ,
,![]() 的两个不同根,
的两个不同根,
∴![]()
(Ⅲ)因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() .∴
.∴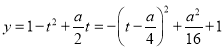
又∵![]() ,由
,由![]() 得
得![]() ,
,
∴![]() .
.
(1)当![]() ,即
,即![]() 时,可知
时,可知![]() 在
在![]() 上为减函数,
上为减函数,
则当![]() 时
时![]() ,
,
由![]() ,解得:
,解得:![]() ,不合题意,舍去.
,不合题意,舍去.
(2)当![]() ,即
,即![]() 时,结合图象可知,当
时,结合图象可知,当![]() 时,
时,![]() ,
,
由![]() ,解得
,解得![]() ,满足题意.
,满足题意.
(3)当![]() ,即
,即![]() 时,知
时,知![]() 在
在![]() 上为增函数,
上为增函数,
则![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,舍去
,舍去
综上,![]() 或
或![]() 为所求.
为所求.

练习册系列答案
相关题目
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分时,才能使
区开设多少个分时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)