��Ŀ����
����Ŀ���ڡ������ۡ�ģʽ�ı����£�ij�������۹�˾���ƹ����·ֵ꣬�ƻ���![]() �е�
�е�![]() ������ֵ꣬Ϊ��ȷ���ڸ�������ֵ�ĸ������ù�˾�Ը����ѿ���ֵ������������������˳���������õ����б���
������ֵ꣬Ϊ��ȷ���ڸ�������ֵ�ĸ������ù�˾�Ը����ѿ���ֵ������������������˳���������õ����б���![]() ��ʾ�ڸ�������ֵ�ĸ�����
��ʾ�ڸ�������ֵ�ĸ����� ![]() ��ʾ���
��ʾ���![]() ���ֵ��������֮�ͣ�
���ֵ��������֮�ͣ�
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
��1���ù�˾�Ѿ��������жϣ��������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ����
�Ĺ�ϵ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2������ù�˾��![]() ����õ���������
����õ���������![]() ����λ������Ԫ����
����λ������Ԫ����![]() ֮��Ĺ�ϵΪ
֮��Ĺ�ϵΪ![]() �����ϣ�1���е����Իع鷽�̣�����ù�˾Ӧ��
�����ϣ�1���е����Իع鷽�̣�����ù�˾Ӧ��![]() ��������ٸ���ʱ������ʹ
��������ٸ���ʱ������ʹ![]() ��ƽ��ÿ���ֵ�����������
��ƽ��ÿ���ֵ�����������
���ο���ʽ�� ![]() ������
������ ��
��
���𰸡�(1) ![]() ;(2) �ù�˾Ӧ����4���ֵ�ʱ���ڸ�����ÿ���ֵ��ƽ���������.
;(2) �ù�˾Ӧ����4���ֵ�ʱ���ڸ�����ÿ���ֵ��ƽ���������.
�����������������
��1�������������ݣ����չ�ʽ����ع鷽���е�ϵ�����ɣ�
��2�����ã�1��������![]() ��ֵ���
��ֵ���![]() ֮��Ĺ���ֵ������
֮��Ĺ���ֵ������![]() ���ɻ�������ʽ�ɵ����ֵ��
���ɻ�������ʽ�ɵ����ֵ��
���������
��1���ɱ������ݺͲο����ݵã� ![]() ��
�� ![]() ��
��
��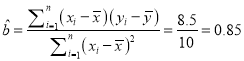 ����
����![]() ��
��
��![]() ��
��
��2�������⣬��֪�������Ԥ��ֵ![]() ��
��![]() ֮��Ĺ�ϵΪ��
֮��Ĺ�ϵΪ�� ![]() ��
��
�����ÿ���ֵ��ƽ������Ϊ![]() ����
����![]() ��
��
��![]() ��Ԥ��ֵ
��Ԥ��ֵ![]() ��
��![]() ֮��Ĺ�ϵΪ
֮��Ĺ�ϵΪ![]() ��
��
��![]() ʱ��
ʱ�� ![]() ȡ�����ֵ��
ȡ�����ֵ��
�ʸù�˾Ӧ����4���ֵ�ʱ���ڸ�����ÿ���ֵ��ƽ���������

����Ŀ����֪����![]() ��
��![]() ��
�� ![]() =2.718����������
=2.718����������
��I�� ��![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��II����![]() ʱ������ʽ
ʱ������ʽ![]() ������
������![]() �������
�������
��ʵ��![]() �����ֵ.
�����ֵ.
����Ŀ��ijͬѧ�á����ģ�ⷽ������������![]() ��ֱ��
��ֱ��![]() ��
�� ![]() ��Χ�ɵ����������ε����ʱ���ü�����ֱ������10��������
��Χ�ɵ����������ε����ʱ���ü�����ֱ������10��������![]() �ϵľ��������
�ϵľ��������![]() ��10������
��10������![]() �ϵľ��������
�ϵľ��������![]() ��
��![]() ��
�� ![]() �������������±���ǰ����.
�������������±���ǰ����.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
�ɴ˿ɵ�������������������һ������ֵ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
