Question

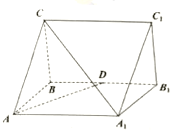
【题目】如图，正三棱柱中，为的中点.

（1）求证：；

（2）若点为四边形内部及其边界上的点，且三棱锥的体积为三棱柱体积的，试在图中画出点的轨迹，并说明理由.

Answer 1

【答案】（1）见解析；（Ⅱ）见解析.

【解析】试题分析：（1）取的中点，连接，首先证明平面得到，在正方形中，利用三角形全等可得，进而得到平面，即可得到结论；（2）取中点，连接，则线段为点的运动轨迹，可通过和证得平面可得结论.

试题解析：（1）证明：取的中点，连接，

∵平面，平面，

∴所以．

∵为正三角形，为的中点，∴，

又∵平面，，

∴平面，

又∵平面，所以

正方形中，∵，∴，

又∵，

∴，故，

又∵，平面，

∴平面，

又∵平面，∴．

（2）取中点，连接，则线段为点的运动轨迹．理由如下．

设三棱锥的高为，

依题意

故．

因为分别为中点，故，又因为平面，平面，

所以平面，所以到平面的距离为．