题目内容
19.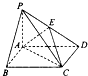 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.(1)求证:平面PDC⊥平面PAD;
(2)求证:PB∥平面EAC;
(3)求直线EC与平面ABCD所成角的正切值.
分析 (1)通过证明PA⊥CD.AD⊥CD,证明CD⊥平面PAD,即可证明平面PDC⊥平面PAD;
(2)证明PB∥EO,即可证明PB∥平面EAC;
(3)设AD的中点为G,连结EG,CG,说明∠ECG为EC与平面ABCD所成的角,在直角三角形ECG中,求解即可.
解答 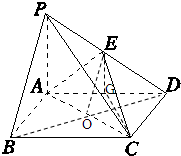 (1)证明:∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
(1)证明:∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
又∵四边形ABCD是矩形,∴AD⊥CD.…(2分)
又PA∩AD=A,PA,AD?平面PAD,∴CD⊥平面PAD.
又∵CD?平面PDC,∴平面PDC⊥平面PAD.…(4分)
(2)连结BD交AC于O,连结OE,
因为E、O分别是PD、BD的中点,
所以PB∥EO,EO?平面EAC,
所以PB∥平面EAC…(7分)
(3)设AD的中点为G,连结EG,CG,
因为E、G分别是PD、AD的中点,
所以PA∥EG,∵PA⊥平面ABCD,
∴EG⊥平面ABCD,
∴∠ECG为EC与平面ABCD所成的角.…(9分)
在直角三角形ECG中,EG=$\frac{1}{2}$PA=1,CG=$\sqrt{D{G}^{2}+D{C}^{2}}$=2$\sqrt{2}$.
所以tan∠ECG=$\frac{EG}{CG}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}$,即所求的正切值为$\frac{\sqrt{2}}{4}$…(12分)
点评 本题考查直线与平面垂直,直线与平面平行的判定定理以及直线与平面市场价的求法,考查计算能力以及空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列函数在其定义域内即是奇函数又是单调递增函数的是( )
| A. | y=-$\frac{1}{x}$ | B. | y=-log2x | C. | y=3x | D. | y=x3 |
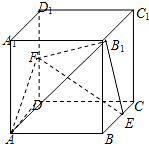 棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.
棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点. 如图,将1,2,3,4任意排成2行2列的田字形数表.
如图,将1,2,3,4任意排成2行2列的田字形数表.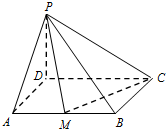 如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.
如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1. 已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.
已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.