题目内容
8.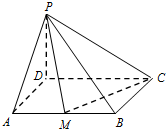 如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.
如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.
分析 以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出实数a的取值.
解答 解: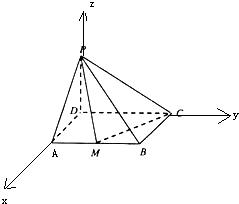 以D为原点,DA为x轴,DC为y轴,DP为z轴,
以D为原点,DA为x轴,DC为y轴,DP为z轴,
建立空间直角坐标系,
设AM=m,DP=t,
则P(0,0,t),M(a,m,0),C(0,2,0),
∴$\overrightarrow{PM}$=(a,m,-t),$\overrightarrow{CM}$=(a,m-2,0),
∵PM⊥CM,
∴$\overrightarrow{PM}$•$\overrightarrow{CM}$=a2+m2-2m=0,
∴a2=-m2+2m=-(m-1)2+1≤1,
∴m=1,a=1边AB上有且只有一点M,使得PM⊥CM,
故答案为:1.
点评 本题考查实数的取值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.已知x>0,y>0,若2y2+8x2-(m2-2m)xy>0恒成立,则实数m的取值范围是( )
| A. | -2<m<4 | B. | -4<m<2 | C. | 2<m<4 | D. | -4<m<4 |
17.已知球的直径SC=4,A,B是该球球面上的两点,∠ASC=∠BSC=30°,且AB=$\sqrt{3}$,则三棱锥S-ABC的体积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
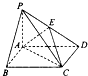 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.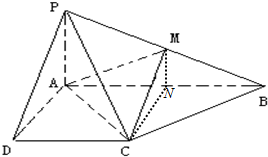 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.