题目内容
已知椭圆的两个焦点F1(-,0),F2(,0),过F1且与坐标轴不平行的直线l1与椭圆相交于M,N两点,△MNF2的周长等于8. 若过点(1,0)的直线l与椭圆交于不同两点P、Q,x轴上存在定点E(m,0),使·恒为定值,则E的坐标为( ▲ )
A. | B. | C. | D. |
C
因为直线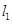 经过点
经过点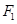 且与椭圆相交于点
且与椭圆相交于点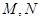 ,而
,而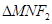 的周长为8
的周长为8
所以 ,解得
,解得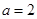 ,故椭圆方程为
,故椭圆方程为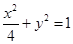
当直线 斜率不存在时,直线
斜率不存在时,直线 方程为
方程为 ,此时
,此时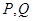 坐标为
坐标为 ,从而有
,从而有
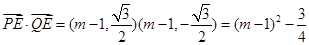
当直线 斜率存在时,设直线
斜率存在时,设直线 方程为
方程为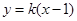 ,联立
,联立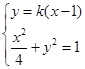 有
有
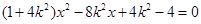
设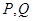 坐标为
坐标为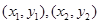 ,则
,则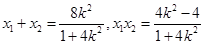
故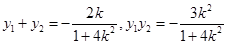
则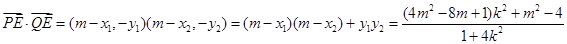 因为
因为 恒为定值,所以
恒为定值,所以 ,解得
,解得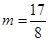
此时 ,符合条件
,符合条件
所以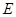 点坐标为
点坐标为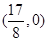 ,故选C
,故选C
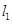 经过点
经过点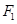 且与椭圆相交于点
且与椭圆相交于点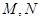 ,而
,而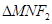 的周长为8
的周长为8所以
 ,解得
,解得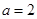 ,故椭圆方程为
,故椭圆方程为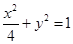
当直线
 斜率不存在时,直线
斜率不存在时,直线 方程为
方程为 ,此时
,此时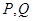 坐标为
坐标为 ,从而有
,从而有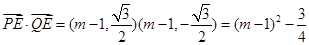
当直线
 斜率存在时,设直线
斜率存在时,设直线 方程为
方程为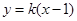 ,联立
,联立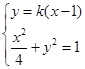 有
有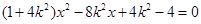
设
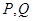 坐标为
坐标为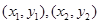 ,则
,则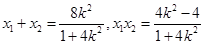
故
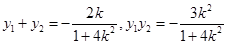
则
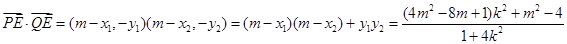 因为
因为 恒为定值,所以
恒为定值,所以 ,解得
,解得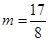
此时
 ,符合条件
,符合条件所以
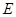 点坐标为
点坐标为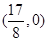 ,故选C
,故选C
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
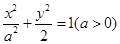 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,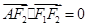 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为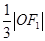 .
.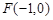 ,交 y轴于点M,若
,交 y轴于点M,若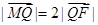 ,求直线l 的斜率.
,求直线l 的斜率.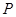 是椭圆
是椭圆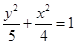 上的一点,
上的一点,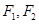 是焦点,且
是焦点,且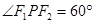 ,则
,则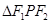 的面积为
的面积为 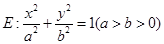 的左右焦点为
的左右焦点为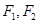 ,过点
,过点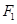 且斜率为正数的直线
且斜率为正数的直线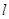 交椭圆
交椭圆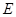 于
于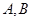 两点,且
两点,且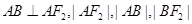 成等差数列。
成等差数列。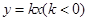 与椭圆
与椭圆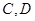 两点,求使四边形
两点,求使四边形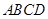 的面积最大时的
的面积最大时的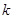 值。
值。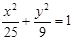 上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若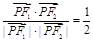 ,则
,则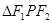 的面积为( )
的面积为( )

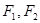 分别为椭圆
分别为椭圆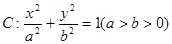 的左、右焦点,点
的左、右焦点,点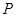 为椭圆上任意一点,
为椭圆上任意一点,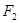 的距离的最大值为
的距离的最大值为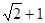 ,且
,且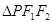 的最大面积为
的最大面积为 .
.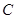 的方程。
的方程。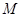 的坐标为
的坐标为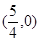 ,过点
,过点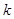 的直线
的直线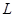 与椭圆
与椭圆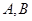 两点。对于任意的
两点。对于任意的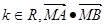 是否为定值?若是求出这个定值;若不是说明理由。
是否为定值?若是求出这个定值;若不是说明理由。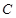 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在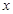 轴上,椭圆上的点到
轴上,椭圆上的点到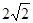 ,离心率
,离心率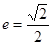 .
.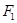 、
、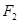 ,过点
,过点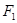 的直线
的直线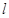 与该椭圆交于点
与该椭圆交于点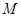 、
、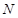 ,
, 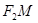 、
、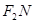 为邻边作平行四边形
为邻边作平行四边形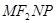 ,求该平行四边形对角线
,求该平行四边形对角线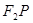 的长度
的长度 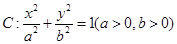 的一个焦点为
的一个焦点为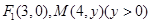 为椭圆上一点,
为椭圆上一点,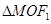 的面积为
的面积为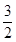
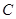 的方程;
的方程;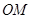 的直线
的直线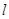 ,使得直线
,使得直线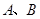 两点,且以线段
两点,且以线段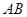 为有经的圆恰好经过原点?若存在,求出
为有经的圆恰好经过原点?若存在,求出 的离心率为( )
的离心率为( )


