题目内容
(本小题满分14分)
设椭圆C: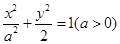 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,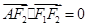 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为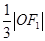 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l 交 x轴于点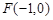 ,交 y轴于点M,若
,交 y轴于点M,若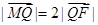 ,求直线l 的斜率.
,求直线l 的斜率.
设椭圆C:
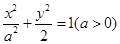 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,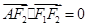 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为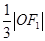 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设Q是椭圆C上的一点,过点Q的直线l 交 x轴于点
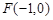 ,交 y轴于点M,若
,交 y轴于点M,若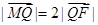 ,求直线l 的斜率.
,求直线l 的斜率.(Ⅰ)由题意知 ,
,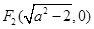 ,其中
,其中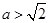 ,
,
由于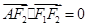 ,则有
,则有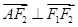 ,
,
所以点A的坐标为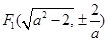 , ……………………………………… 2分
, ……………………………………… 2分
故AF1所在的直线方程为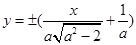 ,
,
所以坐标原点O到直线AF1的距离为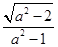 ……………………………… 4分
……………………………… 4分
又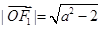 ,所以
,所以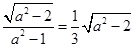 ,解得
,解得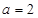 .
.
故所求椭圆C的方程为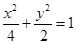 ………………………………………… 7分
………………………………………… 7分
(Ⅱ) 由题意知直线l 的斜率存在.
设直线l 的斜率为k , 直线l 的方程为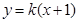 , ……………………… 8分
, ……………………… 8分
则有M(0,k),
设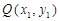 ,由于Q, F,M三点共线,且
,由于Q, F,M三点共线,且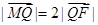 ,
,
根据题意,得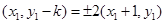 ,
,
解得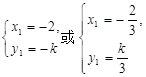 ………………………………………………… 10分
………………………………………………… 10分
又点Q在椭圆上,
所以 ………………………… 13分
………………………… 13分
解得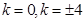 .综上,直线l 的斜率为
.综上,直线l 的斜率为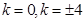 . ………………… 14分
. ………………… 14分
 ,
,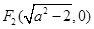 ,其中
,其中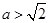 ,
,由于
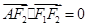 ,则有
,则有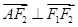 ,
,所以点A的坐标为
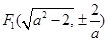 , ……………………………………… 2分
, ……………………………………… 2分故AF1所在的直线方程为
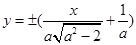 ,
,所以坐标原点O到直线AF1的距离为
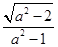 ……………………………… 4分
……………………………… 4分又
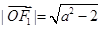 ,所以
,所以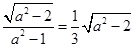 ,解得
,解得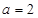 .
.故所求椭圆C的方程为
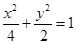 ………………………………………… 7分
………………………………………… 7分(Ⅱ) 由题意知直线l 的斜率存在.
设直线l 的斜率为k , 直线l 的方程为
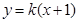 , ……………………… 8分
, ……………………… 8分则有M(0,k),
设
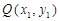 ,由于Q, F,M三点共线,且
,由于Q, F,M三点共线,且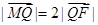 ,
,根据题意,得
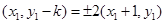 ,
,解得
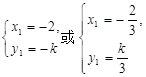 ………………………………………………… 10分
………………………………………………… 10分又点Q在椭圆上,
所以
 ………………………… 13分
………………………… 13分解得
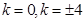 .综上,直线l 的斜率为
.综上,直线l 的斜率为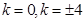 . ………………… 14分
. ………………… 14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
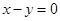 与椭圆
与椭圆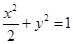 相交A,B两点,点C是椭圆上的动点,则
相交A,B两点,点C是椭圆上的动点,则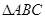 面积的最大值为 。
面积的最大值为 。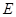 :
: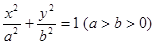 ,设该椭圆上的点到左焦点
,设该椭圆上的点到左焦点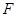
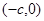 的最大距离为
的最大距离为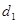 ,到右顶点
,到右顶点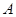
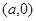 的最大距离为
的最大距离为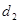 .
.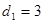 ,
,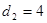 ,求椭圆
,求椭圆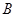
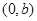 的最大距离为
的最大距离为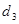 ,求证:
,求证: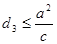 .
.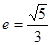 ,一条准线为
,一条准线为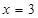 的椭圆的标准方程是________.
的椭圆的标准方程是________. 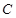 :
: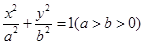 的离心率为
的离心率为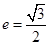 ,且过点
,且过点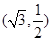 .
.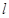 与椭圆
与椭圆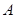 、
、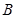 两点,若以
两点,若以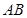 为直径的圆
为直径的圆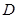 经过坐标原点.证明:圆
经过坐标原点.证明:圆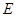 在坐标原点,焦点在
在坐标原点,焦点在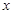 轴上,且经过
轴上,且经过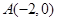 、
、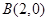 、
、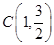 三点.
三点.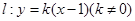 与椭圆
与椭圆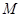 、
、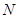 两点.
两点.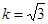 ,求
,求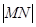 的长;
的长;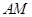 与直线
与直线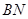 的交点在直线
的交点在直线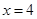 上.
上.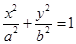
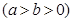 的一个焦点为F(1,0),且过点(2,0)
的一个焦点为F(1,0),且过点(2,0)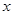 轴,又直线
轴,又直线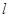 :
:




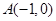 的直线
的直线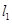 与过点
与过点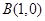 的直线
的直线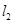 相交于点M,
相交于点M,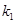 ,
,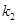 的乘积为定值
的乘积为定值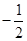 ,求点M的轨迹方程.
,求点M的轨迹方程.