题目内容
(本小题满分12分)
设A1、A2是双曲线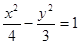 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于 轴的弦,
轴的弦,
(Ⅰ)直线A1P1与A2P2交点P的轨迹 的方程;
的方程;
(Ⅱ)过 与
与 轴的交点Q作直线与(1)中轨迹
轴的交点Q作直线与(1)中轨迹 交于M、N两点,连接FN、FM,其中F
交于M、N两点,连接FN、FM,其中F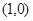 ,求证:
,求证: 为定值;
为定值;
设A1、A2是双曲线
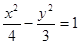 的实轴两个端点,P1P2是双曲线的垂直于
的实轴两个端点,P1P2是双曲线的垂直于 轴的弦,
轴的弦,(Ⅰ)直线A1P1与A2P2交点P的轨迹
 的方程;
的方程;(Ⅱ)过
 与
与 轴的交点Q作直线与(1)中轨迹
轴的交点Q作直线与(1)中轨迹 交于M、N两点,连接FN、FM,其中F
交于M、N两点,连接FN、FM,其中F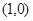 ,求证:
,求证: 为定值;
为定值;(Ⅰ)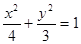 (
(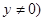 ;(Ⅱ)见解析。
;(Ⅱ)见解析。
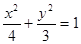 (
(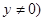 ;(Ⅱ)见解析。
;(Ⅱ)见解析。(Ⅰ)利用交轨法来求直线P1A1和P2A2的交点的轨迹方程,先根据已知条件求出A1、A2点的坐标,设P(x0,y0),则N(x0,-y0),求出直线PA1和NA2的方程,联立方程,方程组的解为直线PA1和NA2交点的坐标,再把P点坐标(x0,y0)用x,y表示,代入双曲线方程,化简即得轨迹C的方程.
(Ⅱ)设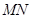 的方程为
的方程为 ,
,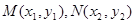 ,直线MN的方程与曲线C的方程联立消y可得关于x的一元二次方程,解出M,N点横坐标之和与之积代入下式
,直线MN的方程与曲线C的方程联立消y可得关于x的一元二次方程,解出M,N点横坐标之和与之积代入下式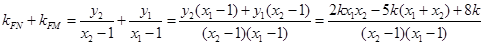 即可证明
即可证明 为定值.
为定值.
(Ⅰ)设 ,则
,则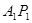 的方程为
的方程为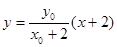 ①
①
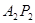 的方程为
的方程为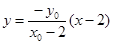 ② 将①×②,得
② 将①×②,得
又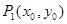 在双曲线上,
在双曲线上,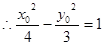 ,即
,即 ,
,
代入上式 ,得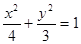 (
(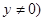 ………5分
………5分
(Ⅱ)法一:设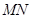 的方程为
的方程为 ,
,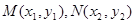
联立,得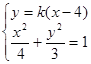 消
消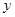 ,得
,得
则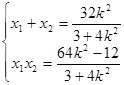
 ..12分
..12分
(Ⅱ)设
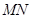 的方程为
的方程为 ,
,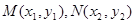 ,直线MN的方程与曲线C的方程联立消y可得关于x的一元二次方程,解出M,N点横坐标之和与之积代入下式
,直线MN的方程与曲线C的方程联立消y可得关于x的一元二次方程,解出M,N点横坐标之和与之积代入下式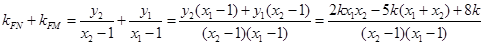 即可证明
即可证明 为定值.
为定值.(Ⅰ)设
 ,则
,则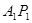 的方程为
的方程为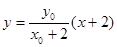 ①
①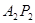 的方程为
的方程为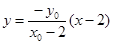 ② 将①×②,得
② 将①×②,得
又
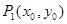 在双曲线上,
在双曲线上,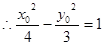 ,即
,即 ,
,代入上式 ,得
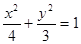 (
(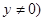 ………5分
………5分 (Ⅱ)法一:设
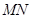 的方程为
的方程为 ,
,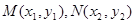
联立,得
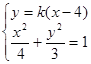 消
消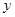 ,得
,得
则
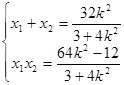
 ..12分
..12分
练习册系列答案
相关题目
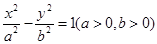 右支上一点,F1、F2分别为双曲线的左、右焦点,I为
右支上一点,F1、F2分别为双曲线的左、右焦点,I为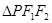 的内心,若
的内心,若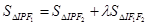 成立,则
成立,则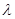 的值为 ( )
的值为 ( )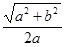
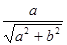
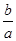
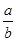
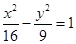 的渐近线方程为_____________.
的渐近线方程为_____________.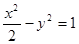 的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点
的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点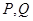 。
。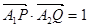 ,求点T的坐标;
,求点T的坐标;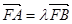 ,若
,若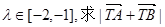 (T为(1)中的点)的取值范围。
(T为(1)中的点)的取值范围。 的实轴长是 ( )
的实轴长是 ( ) 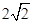
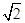
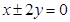 ,焦距为
,焦距为 ,这双曲线的方程为_______________
,这双曲线的方程为_______________ 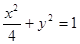 共焦点,则其渐近线方程是 ( )
共焦点,则其渐近线方程是 ( )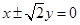
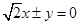
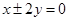
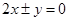
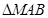 是直角三角形,则此双曲线的离心率e的值为 ( )
是直角三角形,则此双曲线的离心率e的值为 ( )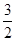
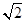
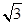
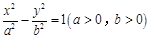 的渐近线方程为
的渐近线方程为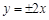 ,则其离心率为( )
,则其离心率为( )