二次函数y=ax2+bx+c的图象是抛物线.其焦点到准线的距离是1.则a的值是$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网——

题目内容

15．二次函数y=ax²+bx+c（a＞0）的图象是抛物线，其焦点到准线的距离是1，则a的值是$\frac{1}{2}$．

分析二次函数y=ax²+bx+c可化为y=a（x+$\frac{b}{2a}$）²-$\frac{{b}^{2}}{4a}$+c，形状与y=ax²相似，利用焦点到准线的距离是1，可得$\frac{1}{2a}$=1，即可求出a的值．

解答解：二次函数y=ax²+bx+c可化为y=a（x+$\frac{b}{2a}$）²-$\frac{{b}^{2}}{4a}$+c，形状与y=ax²相似，
∵焦点到准线的距离是1，∴$\frac{1}{2a}$=1，
∴a=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评本题考查抛物线方程与性质，考查学生的计算能力，属于中档题．

练习册系列答案

导与学学案导学系列答案

地道中考系列答案

地理图册系列答案

第一测评系列答案

点金系列答案

点睛学案系列答案

夺冠金卷单元同步测试系列答案

夺冠课时导学案系列答案

发现会考系列答案

发展性评价系列答案

相关题目

5．已知偶函数f（x）满足，f（x+1）=-f（x）且当x∈[-1，0]时，f（x）=x²，若在区间[-1，3]内，函数g（x）=f（x）-log_a（x+2）有4个零点，则实数a的取值范围是[5，+∞）．

6．在正方体OADB-CA′D′B′中，点E是AB与OD的交点，M是OD′与CE的交点，
（1）试分别用向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$表示向量$\overrightarrow{OD′}$和$\overrightarrow{OM}$；
（2）$\overrightarrow{OI}$，$\overrightarrow{OJ}$，$\overrightarrow{OK}$分别为$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$方向上的单位向量，试用$\overrightarrow{OI}$，$\overrightarrow{OJ}$，$\overrightarrow{OK}$表示$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$．

3．已知圆M与x轴相切且过点（0，2），直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=2+\sqrt{3}t}\end{array}\right.$（t为参数）．
（1）写出直线l的普通方程与圆M的圆心的轨迹方程；
（2）P为直线l上任意一点，Q为C上的任意一点，求P、Q两点间距离的最小值．

10．已知sinα+cosα=$\frac{4}{5}$，且$\frac{3π}{2}$＜α＜2π，计算：
（1）sinα-cosα；
（2）$\frac{1}{co{s}^{2}α}$-$\frac{1}{si{n}^{2}α}$．

20．已知数列{a_n}的前n项和为S_n=pn²-n（p∈R，且p≠0），且a₂，a₃，a₅依次成等比数列．
（1）求数列{a_n}的通项；
（2）若数列{b_n}满足b_n=n•2${\;}^{{a}_{n}}$，求数列{b_n}的前n项和T_n．

7．已知x+2y=2，则$\sqrt{{x}^{2}+{y}^{2}}$+y的最小值为$\frac{\sqrt{155}}{10}$．

4．已知向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（2，-1），点O为坐标原点，若向量$\overrightarrow{OA}=3\overrightarrow{a}-\overrightarrow{b}$，$\overrightarrow{BA}=2\overrightarrow{b}-\overrightarrow{a}$，求向量$\overrightarrow{BO}$的坐标．

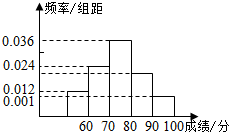对某班的全体学生一次数学测试成绩进行分析，数据的分组情况为：[50，60）[60，70）[70，80）[80，90）[90，100），频率分布直方图如图：
（Ⅰ）求成绩落在[80，90）之间的频率；
（Ⅱ）若低于60分的人数是6人，则该班学生人数是多少？
（Ⅲ）请你估计全班的平均分．