题目内容
20.已知数列{an}的前n项和为Sn=pn2-n(p∈R,且p≠0),且a2,a3,a5依次成等比数列.(1)求数列{an}的通项;
(2)若数列{bn}满足bn=n•2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1)由题意得a2=3p-1,a3=5p-1,a5=9p-1,从而求通项公式;
(2)化简bn=n•2${\;}^{{a}_{n}}$=n•4n-1,从而利用错位相减法求数列的和.
解答 解:(1)a2=S2-S1=4p-2-(p-1)=3p-1,
a3=S3-S2=9p-3-(4p-2)=5p-1,
a5=S5-S4=25p-5-(16p-4)=9p-1,
∵a2,a3,a5依次成等比数列,
∴(5p-1)(5p-1)=(3p-1)(9p-1),
解得,p=1,
故a1=S1=1-1=0,
an=Sn-Sn-1=pn2-n-(p(n-1)2-(n-1))
=(2n-1)p-1=2n-2,
a1=0也满足an=2n-2,
故数列{an}的通项公式为an=2n-2;
(2)bn=n•2${\;}^{{a}_{n}}$=n•4n-1,
故Tn=1+2•4+3•42+…+n•4n-1,
4Tn=1•4+2•42+3•43+…+(n-1)•4n-1+n•4n,
故3Tn=-1-4-42-…-4n-1+n•4n,
故3Tn=n•4n-$\frac{{4}^{n}-1}{4-1}$,
故Tn=$\frac{(3n-1){4}^{n}+1}{9}$.
点评 本题考查了数列的通项公式及前n项和公式的应用及错位相减法的应用.

练习册系列答案
相关题目
10.已知定义在R上的偶函数f(x)是以π为最小正周期的周期函数,且当$x∈[0,\frac{π}{2}]$时,$f(x)=sinx,则f(\frac{8π}{3})$的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.函数y=f(x)=3x+1在点x=2处的瞬时变化率估计是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
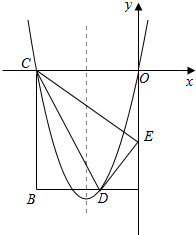 如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.