题目内容
已知函数 在
在 处取得极值
处取得极值 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设 是曲线
是曲线 上除原点
上除原点 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于 轴的直线交曲线于点
轴的直线交曲线于点 ,试问:是否存在这样的点
,试问:是否存在这样的点 ,使得曲线在点
,使得曲线在点 处的切线与
处的切线与 平行?若存在,求出点
平行?若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)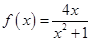 ;(Ⅱ)存在,坐标为
;(Ⅱ)存在,坐标为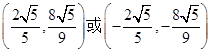 ;(Ⅲ)
;(Ⅲ) 的取值范围是
的取值范围是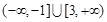 .
.
解析试题分析:(Ⅰ)由题意知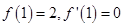 ,解出
,解出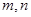 ;(Ⅱ)先假设存在这样的点并设出点的坐标
;(Ⅱ)先假设存在这样的点并设出点的坐标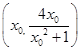 ,然后根据斜率相等列出等式,解得
,然后根据斜率相等列出等式,解得 即可;(Ⅲ)有3中解法,1的基本思路是:先利用导数求得
即可;(Ⅲ)有3中解法,1的基本思路是:先利用导数求得 的最小值,然后说明
的最小值,然后说明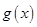 在
在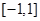 上的最小值不能大于
上的最小值不能大于 的最小值,根据这一条件求得
的最小值,根据这一条件求得 的范围;2的基本思路是:先利用导数求得
的范围;2的基本思路是:先利用导数求得 的最小值-2,要使总存在
的最小值-2,要使总存在 ,使得
,使得 成立,说明
成立,说明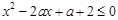 在
在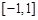 上有解,利用二次函数知识解答;3的基本思路和2有相似地方,只是在说明
上有解,利用二次函数知识解答;3的基本思路和2有相似地方,只是在说明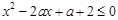 在
在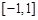 上有解时,不是利用二次函数知识,而是利用换元和分离参数法解答.
上有解时,不是利用二次函数知识,而是利用换元和分离参数法解答.
试题解析:⑴∵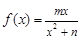 ,∴
,∴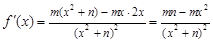 .又
.又 在
在 处取得极值
处取得极值 .
.
∴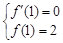 ,即
,即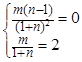 ,解得
,解得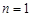 ,
,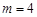 ,经检验满足题意,∴
,经检验满足题意,∴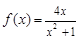 .
.
⑵由⑴知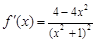 .假设存在满足条件的点
.假设存在满足条件的点 ,且
,且 ,则
,则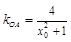 ,
,
又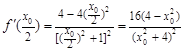 .则由
.则由 ,得
,得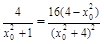 ,∴
,∴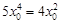 ,∵
,∵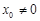 ,
,
∴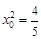 ,得
,得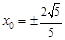 .故存在满足条件的点
.故存在满足条件的点
此时点 的坐标为
的坐标为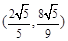 或
或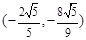 .
.
⑶解法 :
: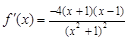 ,令
,令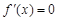 ,得
,得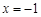 或
或 .
.
当 变化时,
变化时,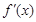 、
、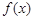 的变化情况如下表:
的变化情况如下表: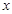
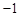
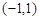

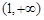
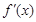
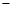


360全优测评系列答案
为了灿烂的明天系列答案
口算心算速算天天练江苏人民出版社系列答案
开心考卷单元测试卷系列答案

驿站新跨越系列答案
黄冈小状元培优周课堂系列答案
小学期中期末培优卷系列答案

双基同步导学导练系列答案
 (
( 为实常数).
为实常数). 时,证明:
时,证明: 不是奇函数;②
不是奇函数;② 是
是 上的单调递减函数.
上的单调递减函数. 与
与 的值.
的值. 为奇函数.
为奇函数. ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明); ,使
,使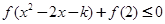 ,求实数k的最大值.
,求实数k的最大值. 是定义在
是定义在 上的减函数,满足
上的减函数,满足 .
. ;
; ,解不等式
,解不等式 .
. 是定义在
是定义在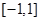 上的奇函数,且
上的奇函数,且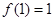 ,若
,若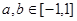 ,
,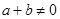 有
有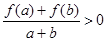 恒成立.
恒成立.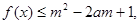 对所有
对所有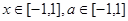 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; 的单调性,并证明.
的单调性,并证明.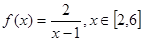 ,试判断此函数
,试判断此函数 在
在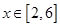 上的单调性,并求此函数
上的单调性,并求此函数 ,函数
,函数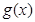
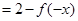 .
.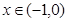 时,
时,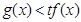 恒成立,求实数
恒成立,求实数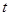 的最大值.
的最大值.