Question

【题目】已知直线 与椭圆 有且只有一个公共点 .
（1）求椭圆C的标准方程;
（2）若直线 交C于A,B两点,且OA⊥OB(O为原点),求b的值.

Answer 1

【答案】
（1）解：由 在椭圆上,可得 ①,
由直线与椭圆有且只有一个公共点,则
,消去 可得 ,
由题意可得 ,即为 ②,
由①②,且 ,解得 ,即有椭圆方程为
（2）解：设 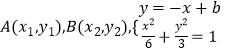消去 ,可得 ,
判别式
由 即为 ,则
解得 或 ，代入判别式符合要求,则 或
【解析】本题主要考查椭圆的标准方程的求法以及直线与椭圆的位置关系。（1）联立直线与椭圆方程，利用有一个交点说明判别式=0即可。（2）联立方程，因为有两个交点，所以判别式大于0，以及根据垂直得到向量的数量积为0即可。
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．