题目内容
已知抛物线的方程为 ,直线
,直线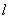 的方程为
的方程为 ,点A
,点A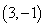 关于直线
关于直线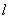 的对称点在抛物线上.
的对称点在抛物线上.
(1)求抛物线的方程;
(2)已知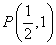 ,点
,点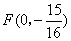 是抛物线的焦点,M是抛物线上的动点,求
是抛物线的焦点,M是抛物线上的动点,求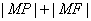 的最小值及此时点M的坐标;
的最小值及此时点M的坐标;
(3)设点B、C是抛物线上的动点,点D是抛物线与 轴正半轴交点,△BCD是以D为直角顶点的直角三角形.试探究直线BC是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
轴正半轴交点,△BCD是以D为直角顶点的直角三角形.试探究直线BC是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
解:(1)设点A(3,-1)关于直线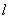 的对称点为坐标为
的对称点为坐标为 (x,y),
(x,y),
 则
则 解得
解得 -
-
把点 (1,3)代入
(1,3)代入 ,解得a = 4,
,解得a = 4,
所以抛物线的方程为
(2)∵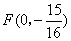 是抛物线的焦点,抛物线的顶点为(0,-1),
是抛物线的焦点,抛物线的顶点为(0,-1),
∴抛物线的准线为 ,
,
过点M作准线的垂线,垂足为A,由抛物线的定义知 ,
,
∴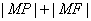 =
= ,当且仅当P、M、A三点共线时“=”成立,
,当且仅当P、M、A三点共线时“=”成立,
即当点M为过点P所作的抛物线准线的垂线与抛物线的交点时,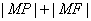 取最小值,
取最小值,
∴ ,这时点M的坐标为
,这时点M的坐标为 .
.
(3)BC所在的直线经过定点,该定点坐标为 ,
,
令 ,可得D点的坐标为
,可得D点的坐标为
设 ,显然
,显然 ,
,
则 -
-

∵ ,∴
,∴ ,即
,即
直线BC的方程为
即 -
-
所以直线BC经过定点 .-
.-

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
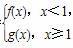 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.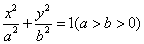 上一点,F1、F2分别是椭圆的左右焦点,I为△PF1F2的
上一点,F1、F2分别是椭圆的左右焦点,I为△PF1F2的 、
、 的坐标满足不等式组
的坐标满足不等式组 ,若
,若 ,则
,则 的取值范围是
的取值范围是 B.
B.  C.
C.  D.
D. 
 是圆O的切线,切点为
是圆O的切线,切点为 ,
, 交圆
交圆 于
于 两点,且
两点,且 则
则 的长为 .
的长为 .
 的正方形,俯视图
的正方形,俯视图 A.
A. B.
B. 
 D.
D.
 是圆
是圆 的直径,
的直径, ,
, 为圆
为圆 .若
.若 ,则
,则


 ,若
,若 恒成立,则
恒成立,则 的取值范围是
的取值范围是 (B)
(B) (C)
(C) (D)
(D)
 ,则以下四个命题中正确的是( )
,则以下四个命题中正确的是( ) ②
②
 ④
④