题目内容
已知椭圆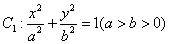 的离心率与双曲线
的离心率与双曲线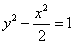 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆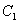 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆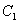 的方程;
的方程;
(2)设椭圆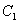 的左焦点为
的左焦点为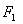 ,右焦点为
,右焦点为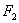 ,直线
,直线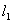 过点
过点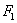 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线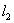 垂直
垂直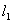 于点
于点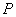 ,线段
,线段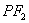 垂直平分线交
垂直平分线交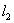 于点
于点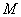 ,求点
,求点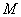 的轨迹
的轨迹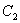 的方程;
的方程;
(3)设第(2)问中的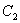 与
与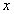 轴交于点
轴交于点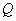 ,不同的两点
,不同的两点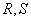 在
在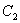 上,且满足
上,且满足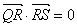 ,求
,求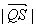 的取值范围.
的取值范围.

 动点
动点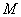 到定直线
到定直线 的距离等于它到定点
的距离等于它到定点 的距离 5分
的距离 5分
 动点
动点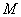 的轨迹
的轨迹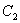 是以
是以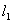 为准线,
为准线,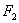 为焦点的抛物线, 6分
为焦点的抛物线, 6分
 点
点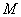 的轨迹
的轨迹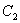 的方程为
的方程为 . 7分
. 7分
(3)由(2)知: ,设
,设 , 则
, 则 , 8分
, 8分

 , 9分
, 9分
由 ,左式可化简为:
,左式可化简为: , 10分
, 10分
 ,
,
当且仅当 ,即
,即 时取等号, 11分
时取等号, 11分
又 ,
,
 当
当 ,即
,即 时,
时, , 13分
, 13分
故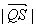 的取值范围是
的取值范围是 . 14分
. 14分

练习册系列答案
相关题目
 则这个三棱柱的体积为 ( )
则这个三棱柱的体积为 ( )
 D.12
D.12 是首项和公比均为
是首项和公比均为 的等比数列,设
的等比数列,设 .
.
 是等差数列;
是等差数列; 数列
数列 .
.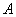 在抛物线
在抛物线 上,且点
上,且点 的距离为
的距离为 ,则点
,则点 B.
B. C.
C. D.
D.
 ABC是边长为l的等边三角形,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将
ABC是边长为l的等边三角形,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将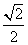 .
.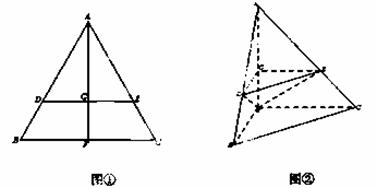
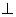 平面ABF;
平面ABF;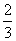 时,求三棱锥F-DEG的体积
时,求三棱锥F-DEG的体积
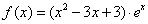 .
.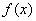 的单调区间;
的单调区间;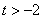 时,判断
时,判断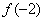 和
和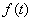 的大小,并说明理由;
的大小,并说明理由;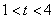 时,关于
时,关于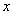 的方程:
的方程: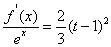 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
, ,
, ,则
,则 、
、 、
、 的大小关系是( )
的大小关系是( ) B.
B.
 D.
D.
 B.
B. C.
C. D.
D.
 (其中A>0,
(其中A>0, )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象( )
的图象,则只需将g(x)=sin2x的图象( )
 个长度单位 B. 向左平移
个长度单位 B. 向左平移 个长度单位 D. 向左平移
个长度单位 D. 向左平移