题目内容
3．在数列{an}中，an+1=can（c为非零常数），前n项和为Sn=3n-2+k，则实数k的值为（ ）| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{1}{9}$ | D． | -$\frac{1}{9}$ |
分析 由已知得数列{an}是等比数列，利用${a}_{n}=\left\{\begin{array}{l}{{S}_{1}，n=1}\\{{S}_{n}-{S}_{n-1}，n≥2}\end{array}\right.$求出前3项，利用等比数列的性质能求出k．
解答 解：∵在数列{an}中，an+1=can（c为非零常数），前n项和为Sn=3n-2+k，
∴数列{an}是等比数列，
∴${a}_{1}={S}_{1}=\frac{1}{3}+k$，
a2=S2-S1=（1+k）-（$\frac{1}{3}+k$）=$\frac{2}{3}$，
a3=S3-S2=（3+k）-（1+k）=2，
∴由${{a}_{2}}^{2}={a}_{1}{a}_{3}$，得$\frac{4}{9}=（\frac{1}{3}+k）•2$，
解得k=-$\frac{1}{9}$．
故选：D．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
14．已知a＞0，x、y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a（x-3）}\end{array}\right.$ 若z=2x+y的最小值与最大值的和为7，则a=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
8．sin4$\frac{π}{12}$-cos4$\frac{π}{12}$等于（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
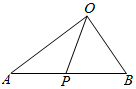如图，在△AOB中，点P在AB上，且$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$（m∈R），求$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$的值．
12．已知集合A={y|y=（$\frac{1}{2}$）x，x≥-1}，B={y|y=ex+1，x≤0}，则下列结论正确的是（ ）
| A． | A=B | B． | A∪B=R | C． | A∩（∁RB）=∅ | D． | B∩（∁RA）=∅ |