题目内容
定长为3的线段AB的端点A、B在抛物线y2=x上移动,求AB中点到y轴距离的最小值,并求出此时AB中点M的坐标.
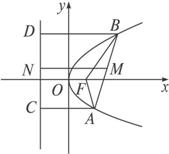
解:如图,设F是抛物线y2=x的焦点,A、B两点到准线的垂线分别是AC、BD,M点到准线的垂线为MN,N为垂足,则|MN|=![]() (|AC|+|BD|),
(|AC|+|BD|),
根据抛物线定义得:|AC|=|AF|,|BD|=|BF|,
∴|MN|=![]() (|AF|+|BF|)≥
(|AF|+|BF|)≥![]() .
.
设M点的横坐标为x,则:|MN|=x+![]() .∴x=|MN|-
.∴x=|MN|-![]() ≥
≥![]() -
-![]() =
=![]() .
.
等号成立的条件是弦AB过点F,由于|AB|>2p=1,
∴AB过焦点是可能的,此时M点到y轴最短距离是![]() ,即AB的中点横坐标为
,即AB的中点横坐标为![]() .当F在AB上时,设A、B的纵坐标分别为y1、y2,则y1y2=-p2=-
.当F在AB上时,设A、B的纵坐标分别为y1、y2,则y1y2=-p2=-![]() ,从而(y1+y2)2=y12+y22+2y1y2=2×
,从而(y1+y2)2=y12+y22+2y1y2=2×![]() -
-![]() =2.
=2.
∴y1+y2=±![]() ,∴此时AB中点的纵坐标为±
,∴此时AB中点的纵坐标为±![]() ,
,
∴M的坐标为(![]() ,±
,±![]() )时,M到y轴距离的最小值为
)时,M到y轴距离的最小值为![]() .
.
点拨:此题的难点是求最小值.而利用抛物线定义及梯形中位线性质等几何知识使问题变得非常简单,这再一次说明在解题中注意运用圆锥曲线的定义及有关的几何知识,对解题是非常有益的.

练习册系列答案
相关题目
 =x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.
=x上移动,AB的中点为M,求点M到y轴的最短距离,并求出此时点M的坐标.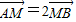 .
.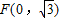 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.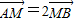 .
.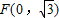 且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.
且不垂直于坐标轴的动直线l交轨迹C于A、B两点,问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明.