题目内容
19．函数y=x3-3x-a有三个相异的零点，则a的取值范围是（ ）| A． | [2，+∞） | B． | [-2，2] | C． | （-2，2） | D． | （-∞，-2] |
分析 求出函数的导数，运用导数判断出极值，根据图象求解出a的范围即可．
解答 解：函数y=x3-3x-a，
y′=3x2-3，
∴y′=3x2-3=0，x=±1，
y′=3x2-3＞0，x＞1，x＜-1，
y′=3x2-3＜0，-1＜x＜1，
∴函数在（-1，1）单调递减，（1，+∞）（-∞，-1）单调递增，
∴f（x）极大值=f（-1）=2-a，
f（x）极小值=f（2）=-2-a
∴使得函数f（x）=x3-3x-a有三个零点，必须：$\left\{\begin{array}{l}{2-a＞0}\\{-2-a＜0}\end{array}\right.$，解得a∈（-2，2）．
故选：C．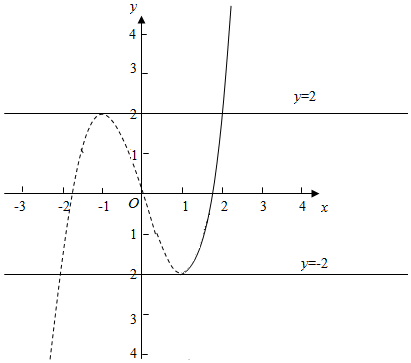
点评 本题考查了函数的图象的运用，结合导数判断极值，考查数形结合思想的应用，属于综合题，难度较大．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，∠ABC=90°，AB=$\sqrt{3}$，BC=1，P在平面ABC内，且为△ABC外一点，∠BPC=90°
14．数列1+$\frac{1}{2}$，2+$\frac{1}{4}$，3+$\frac{1}{8}$，4+$\frac{1}{16}$，…，的前n项和为（ ）
| A． | $\frac{n（n+1）}{2}$+1-2n | B． | $\frac{n（n+1）}{2}$+1-2-n | C． | $\frac{n（n-1）}{2}$+1-2-n | D． | $\frac{n（n-1）}{2}$+1-2n |
4．由直线x=-$\frac{π}{6}$，x=$\frac{π}{6}$，y=0与直线y=cosx所围成的封闭图形的面积为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD为梯形，AB∥DC，平面PAD⊥平面ABCD，已知BD=2AD=4，AB=2DC=2$\sqrt{5}$，点M在PC上，PM=mMC．