题目内容
已知等差数列{an}的公差大于0，且a3，a5是方程x2－14x＋45＝0
的两根，数列{bn}的前n项的和为Sn，且Sn＝1－
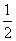bn.
(1)求数列{an}，{bn}的通项公式；
(2)记cn＝an·bn，求证：cn＋1≤cn.
(1)解析：因为a3，a5是方程x2－14x＋45＝0的两根，且数列{an}的公差d>0，
∴a3＝5，a5＝9，公差d＝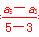
＝2.
∴an＝a5＋(n－5)d＝2n－1(n∈N*)．
又当n＝1时，有b1＝S1＝1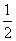－b1，∴b1＝
.
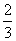当n≥2时，有bn＝Sn－Sn－1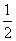＝(bn－1－bn
)，
∴
＝
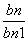(n≥2)，
∴数列{bn}是等比数列，b1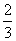＝，q＝.
∴bn＝b1qn－1＝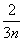
(n∈N*)．
(2)证明：由(1)知cn＝anbn＝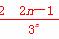
，cn＋1＝
，
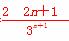∴cn＋1－cn＝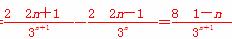
≤0.
∴cn＋1≤cn.
练习册系列答案
科学实验活动册系列答案
相关题目
an，则数列的通项公式an＝________.
＝ad－bc，若数列{an}满足
＝1且
＝12(n∈N*)，则a3＝________，数列{an}的通项公式为an＝________.
必要不充分条件
D．既不充分也不必要条件
上，α为曲线在P处的切线的倾斜角，则α的取值范围为( )
；
(k为常数，e＝2.71828…是自然对数的底数)，曲线y＝f(x)在点(1，f(1))处的切线与x轴平行．