题目内容
(本小题满分16分)
对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(1)当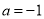 ,
, 时, 判断函数
时, 判断函数 和
和 是否相切?并说明理由;
是否相切?并说明理由;
(2)已知 ,
, ,且函数
,且函数 和
和 相切,求切点P的坐标;
相切,求切点P的坐标;
(3)设 ,点P的坐标为
,点P的坐标为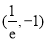 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
(本小题满分16分)
对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(1)当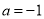 ,
, 时, 判断函数
时, 判断函数 和
和 是否相切?并说明理由;
是否相切?并说明理由;
(2)已知 ,
, ,且函数
,且函数 和
和 相切,求切点P的坐标;
相切,求切点P的坐标;
(3)设 ,点P的坐标为
,点P的坐标为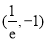 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
 名校课堂系列答案
名校课堂系列答案