题目内容
(本小题满分14分)
如图所示,已知圆 ,
,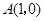 为定点,
为定点, 为圆
为圆 上的动点,线段
上的动点,线段 的垂直平分线交
的垂直平分线交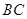 于点
于点 ,点
,点 的轨迹为曲线E.
的轨迹为曲线E.

(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)过点 作直线
作直线 交曲线
交曲线 于
于 两点,设线段
两点,设线段 的中垂线交
的中垂线交 轴于点
轴于点 ,求实数m的取值范围.
,求实数m的取值范围.
如图所示,已知圆
 ,
,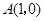 为定点,
为定点, 为圆
为圆 上的动点,线段
上的动点,线段 的垂直平分线交
的垂直平分线交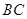 于点
于点 ,点
,点 的轨迹为曲线E.
的轨迹为曲线E.
(Ⅰ)求曲线
 的方程;
的方程;(Ⅱ)过点
 作直线
作直线 交曲线
交曲线 于
于 两点,设线段
两点,设线段 的中垂线交
的中垂线交 轴于点
轴于点 ,求实数m的取值范围.
,求实数m的取值范围.(Ⅰ)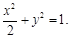 ;(Ⅱ)
;(Ⅱ)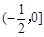 .
.
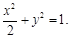 ;(Ⅱ)
;(Ⅱ)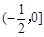 .
. 本试题主要是考查了直线与椭圆的位置关系的运用,以及椭圆方程的求解的综合运用。
(1)因为由题意知,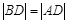 .
.
又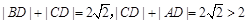 ,
,
∴动点D的轨迹是以点 为焦点的椭圆
为焦点的椭圆
(2)根据已知条件设出直线方程,对于斜率要分类讨论是否存在,然后结合直线方程与椭圆方程联立方程组,结合韦达定理和中点公式得到中垂线方程求解。
解:(Ⅰ)由题意知,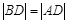 .
.
又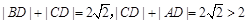 ,
,
∴动点D的轨迹是以点 为焦点的椭圆,且椭圆的长轴长
为焦点的椭圆,且椭圆的长轴长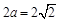 ,
,
焦距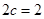 .
. 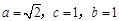 ,
,
∴曲线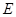 的方程为
的方程为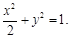 6分
6分
(Ⅱ)①当 的斜率不存在时,线段
的斜率不存在时,线段 的中垂线为
的中垂线为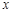 轴,
轴,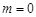 ; 8分
; 8分
②当 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为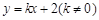 ,代入
,代入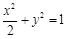
得:
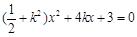 ,由
,由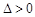 得,
得,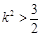 10分
10分
设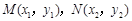 ,则
,则 ,
,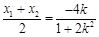 ,
,
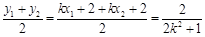 ,
,
∴线段 的中点为
的中点为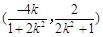 ,中垂线方程为
,中垂线方程为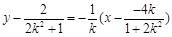 ,12分
,12分
令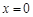 得
得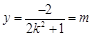 . 由
. 由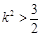 ,易得
,易得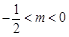 .
.
综上可知,实数m的取值范围是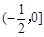 . 14分
. 14分
(1)因为由题意知,
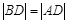 .
. 又
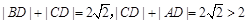 ,
,∴动点D的轨迹是以点
 为焦点的椭圆
为焦点的椭圆(2)根据已知条件设出直线方程,对于斜率要分类讨论是否存在,然后结合直线方程与椭圆方程联立方程组,结合韦达定理和中点公式得到中垂线方程求解。
解:(Ⅰ)由题意知,
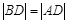 .
. 又
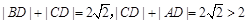 ,
,∴动点D的轨迹是以点
 为焦点的椭圆,且椭圆的长轴长
为焦点的椭圆,且椭圆的长轴长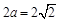 ,
,焦距
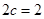 .
. 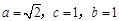 ,
,∴曲线
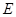 的方程为
的方程为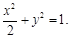 6分
6分(Ⅱ)①当
 的斜率不存在时,线段
的斜率不存在时,线段 的中垂线为
的中垂线为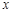 轴,
轴,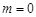 ; 8分
; 8分②当
 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为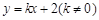 ,代入
,代入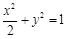
得:
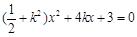 ,由
,由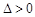 得,
得,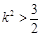 10分
10分设
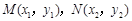 ,则
,则 ,
,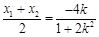 ,
,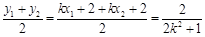 ,
,∴线段
 的中点为
的中点为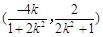 ,中垂线方程为
,中垂线方程为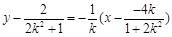 ,12分
,12分令
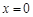 得
得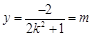 . 由
. 由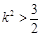 ,易得
,易得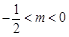 .
. 综上可知,实数m的取值范围是
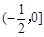 . 14分
. 14分
练习册系列答案
相关题目
 ,
, 所连线段为直径的圆的方程是
所连线段为直径的圆的方程是  和圆
和圆 交于
交于 两点,且
两点,且 , 则
, 则  _______。
_______。 与圆
与圆 的交点,且圆M的圆心到直线
的交点,且圆M的圆心到直线 的距离为
的距离为 ,求圆M的方程.
,求圆M的方程.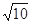
 的圆心在直线
的圆心在直线 上,且圆
上,且圆 轴相切,若圆
轴相切,若圆 得弦长为
得弦长为 ,求圆
,求圆 ,且过点
,且过点 的圆的方程为 .
的圆的方程为 . (2,-1)为圆
(2,-1)为圆 的弦AB的中点,则直线
的弦AB的中点,则直线 的方程为
的方程为



 (a≠1,a∈R),则该圆系恒过定点 .
(a≠1,a∈R),则该圆系恒过定点 .