题目内容
已知极坐标系的极点在直角坐标系的原点处,极轴与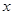 轴的正半轴重合.
轴的正半轴重合.
直线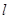 的参数方程为:
的参数方程为: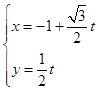 (t为参数),曲线
(t为参数),曲线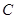 的极坐标方程为:
的极坐标方程为: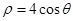 .
.
(Ⅰ)写出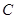 的直角坐标方程,并指出
的直角坐标方程,并指出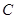 是什么曲线;
是什么曲线;
(Ⅱ)设直线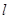 与曲线
与曲线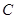 相交于
相交于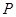 、
、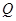 两点,求
两点,求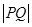 值.
值.
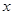 轴的正半轴重合.
轴的正半轴重合.直线
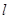 的参数方程为:
的参数方程为: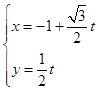 (t为参数),曲线
(t为参数),曲线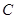 的极坐标方程为:
的极坐标方程为: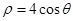 .
.(Ⅰ)写出
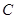 的直角坐标方程,并指出
的直角坐标方程,并指出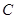 是什么曲线;
是什么曲线;(Ⅱ)设直线
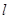 与曲线
与曲线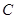 相交于
相交于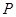 、
、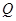 两点,求
两点,求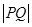 值.
值.(Ⅰ)曲线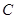 的直角坐标方程为
的直角坐标方程为 ,它是以
,它是以 为圆心,
为圆心,
半径为 的圆.
的圆.
(Ⅱ) 。
。
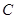 的直角坐标方程为
的直角坐标方程为 ,它是以
,它是以 为圆心,
为圆心,半径为
 的圆.
的圆.(Ⅱ)
 。
。试题分析:(Ⅰ)
 ,
, ,………………………………………………………………2分
,………………………………………………………………2分由
 得:
得:
所以曲线
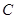 的直角坐标方程为
的直角坐标方程为 ,…………………………4分
,…………………………4分它是以
 为圆心,半径为
为圆心,半径为 的圆. …………………………………………5分
的圆. …………………………………………5分(Ⅱ)把
 代入
代入 整理得
整理得 ,……7分
,……7分设其两根分别为
 、
、 ,则
,则 ,…………………………8分
,…………………………8分 ……………………………………10分
……………………………………10分另解:
化直线参数方程为普通方程,然后求圆心到直线距离,再用垂径定理求得
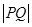 的值.
的值.点评:中档题,学习参数方程、极坐标,其中一项基本的要求是几种不同形式方程的互化,其次是应用极坐标、参数方程,简化解题过程。参数方程的应用,往往可以把曲线问题转化成三角问题,也可在计算弦长时发挥较好作用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中圆
中圆 的参数方程为:
的参数方程为:  ,(
,( 为参数),以
为参数),以 为极轴建立极坐标系,直线极坐标方程为:
为极轴建立极坐标系,直线极坐标方程为: 则圆
则圆
 (
( 为参数)等价的普通方程为( )
为参数)等价的普通方程为( )




 中,曲线
中,曲线 与
与 的交点的极坐标为________
的交点的极坐标为________
 恒成立,则实数a的取值范围______
恒成立,则实数a的取值范围______ 满足
满足 ,
, ,那么
,那么  的最大值是 ( )
的最大值是 ( )


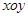 中,曲线
中,曲线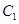 的参数方程为
的参数方程为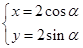 (
(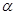 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系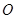 为极点,以
为极点,以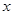 轴为极轴)中,曲线
轴为极轴)中,曲线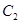 的方程
的方程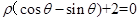 ,
,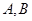 ,则公共弦
,则公共弦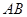 的长是 .
的长是 . (
( 为参数且
为参数且 ,
, ,
, )
)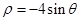 和
和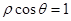 相交于点
相交于点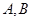 ,则线段
,则线段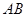 的长度为 .
的长度为 . 是曲线
是曲线 上的动点,则
上的动点,则 的最大值是_________
的最大值是_________