题目内容
(坐标系与参数方程选做题)极坐标系中,曲线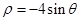 和
和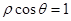 相交于点
相交于点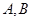 ,则线段
,则线段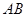 的长度为 .
的长度为 .
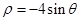 和
和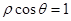 相交于点
相交于点 ,则线段
,则线段 的长度为 .
的长度为 .
试题分析:由题意可知

故该试题求解的弦长AB的值,即可以通过圆的半径2,圆心为(0,-2),得到圆心到直线x=1的距离d=
 ,结合半弦长和半径和弦心距的勾股定理得到线段
,结合半弦长和半径和弦心距的勾股定理得到线段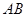 的长度为
的长度为 ,故填写
,故填写
点评:解决该试题的关键是能将极坐标方程化为直角坐标方程,利用点到直线的距离公式和勾股定理得到AB的长度。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则极点到该直线的距离是 .
,则极点到该直线的距离是 . 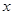 轴的正半轴重合.
轴的正半轴重合. 的参数方程为:
的参数方程为: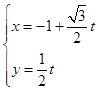 (t为参数),曲线
(t为参数),曲线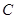 的极坐标方程为:
的极坐标方程为: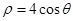 .
.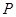 、
、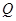 两点,求
两点,求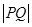 值.
值. (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长. 的参数方程是
的参数方程是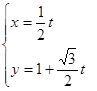 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是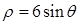 ,则
,则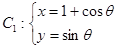
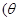 为参数
为参数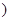 ,在曲线
,在曲线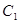 上求一点
上求一点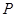 ,使它到直线
,使它到直线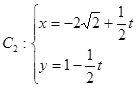
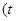 为参数
为参数 (t为参数)焦点为F,则抛物线上的点M(2,m)到F的距离|MF|为( )
(t为参数)焦点为F,则抛物线上的点M(2,m)到F的距离|MF|为( ) 截曲线
截曲线 (
( 为参数)的弦长为___________
为参数)的弦长为___________