题目内容
18．现将5张连号的电影票分给甲、乙等5个人，每人一张，且甲、乙分得的电影票连号，则共有不同分法的种数为（ ）| A． | 12 | B． | 24 | C． | 36 | D． | 48 |
分析 根据题意，分3步进行分析：①、将电影票分成4组，其中1组是2张连在一起，②、将连在一起的2张票分给甲乙，③、将剩余的3张票全排列，分给其他三人，求出每一步的情况数目，由分步计数原理计算可得答案．
解答 解：根据题意，分3步进行分析：
①、将电影票分成4组，其中1组是2张连在一起，有4种分组方法，
②、将连在一起的2张票分给甲乙，考虑其顺序有A22=2种情况，
③、将剩余的3张票全排列，分给其他三人，有A33=6种分法，
则共有4×2×6=48种不同分法，
故选：D．
点评 本题考查排列、组合的实际应用，注意先满足“甲、乙分得的电影票连号”的条件．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线与直线l：x-y+2=0平行，则双曲线C的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{10}$ |
9．（1-$\sqrt{x}$）6（1-$\root{3}{x}$）4的展开式中，x2的系数是（ ）
| A． | -75 | B． | -45 | C． | 45 | D． | 75 |
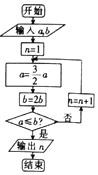名著《算学启蒙》中有如下题：“松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等”．这段话的意思是：“松有五尺长，竹有两尺长，松每天增长前一天长度的一半，竹每天增长前一天长度的两倍．”．为了研究这个问题，以a代表松长，以b代表竹长，设计了如图所示的程序框图，输入的a，b的值分别为5，2，则输出的n的值为（ ）
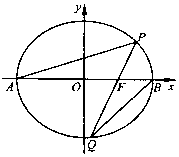如图，在平面直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A，B，过右焦点F的直线l与椭圆C交于P，Q两点（点P在x轴上方）．
3．将函数f（x）=cos2x图象上所有点向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，若g（x）在区间[0，a]上单调递增，则实数a的最大值为（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{3}{4}π$ |