题目内容

已知△ABC中∠BAC=60°，AC=1，AB=2，设点P、Q满足 $数学公式$ ，若 $数学公式$ ，则λ=________．

$\text{[math]}$
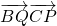分析：由正弦定理可得C=90°，进而可得 $\text{[math]}$ =1，而由数量积的运算可得 $\text{[math]}$ =（λ-1）-4λ+λ-λ²+1= $\text{[math]}$ ，解这个关于λ的方程即可．
解答：在△ABC中∠BAC=60°，
故∠B=180°-（60°+∠C）=120°-∠C，
由正弦定理可得 $\text{[math]}$ ，即sinC=2sinB，
故sinC=2sin（120°-C）=2（ $\text{[math]}$ ）
= $\text{[math]}$ ，解得cosC=0，故C=90°
∴ $\text{[math]}$ =2×1× $\text{[math]}$ =1，
而 $\text{[math]}$ =（ $\text{[math]}$ ）•（ $\text{[math]}$ ）
=[ $\text{[math]}$ - $\text{[math]}$ ]•[λ $\text{[math]}$ ]
=（λ-1） $\text{[math]}$ -λ $\text{[math]}$ +[（1-λ）λ+1] $\text{[math]}$
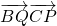=（λ-1）-4λ+λ-λ²+1= $\text{[math]}$ ，
整理可得4λ²+8λ-5=0，即（2λ+5）（2λ-1）=0，
解得λ= $\text{[math]}$ 或 $\text{[math]}$ ，
故答案为： $\text{[math]}$ 或 $\text{[math]}$
点评：本题考查平面向量数量积的运算，涉及正弦定理和一元二次方程的解法，属中档题．