题目内容
10.已知数列{an}的各项均为正数,满足a1=1,ak+1-ak=ai.(i≤k,k=1,2,3,…,n-1)(Ⅰ)求证:${a_{k+1}}-{a_k}≥1\begin{array}{l}{\;}{(k=1,2,3,…,n-1)}\end{array}$;
(Ⅱ)若{an}是等比数列,求数列{an}的通项公式;
(Ⅲ)设数列{an}的前n项和为Sn,求证:$\frac{1}{2}n(n+1)≤{S_n}≤{2^n}-1$.
分析 (I)利用数列的单调性即可证明;
(II)利用递推关系、等比数列的通项公式即可得出;
(III)利用“累加求和”与不等式的性质即可得出.
解答 (Ⅰ)证明:∵ak+1-ak=ai>0(i≤k,k=1,2,3,…,n-1),
∴数列{an}是递增数列,即1<a2<a3<…<an.
又∵ak+1-ak=ai≥1(i≤k,k=1,2,3,…,n-1),
∴ak+1-ak≥1(k=1,2,3,…,n-1).
(Ⅱ)解:∵a2-a1=a1,∴a2=2a1;
∵{an}是等比数列,∴数列{an}的公比为2.
∵ak+1-ak=ai(i≤k,k=1,2,3,…,n-1),∴当i=k时有ak+1=2ak.
这说明在已知条件下,可以得到唯一的等比数列.
∴${a_n}={2^{n-1}}$.
(Ⅲ)证明:∵1=a1=1,2=a2=2,$3≤{a_3}≤{2^2}$,$4≤{a_4}≤{2^3}$,…,$n≤{a_n}≤{2^{n-1}}$,
由上面n个式子相加,得到:$1+2+3+…+n≤{a_1}+{a_2}+{a_3}+…+{a_n}≤{2^0}+{2^1}+{2^2}+…+{2^{n-1}}$,
化简得 $\frac{n(n+1)}{2}<({a_1}+{a_2}+{a_3}+…+{a_n})<({2^n}-1)$,
∴$\frac{1}{2}n(n+1)≤{S_n}≤{2^n}-1$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、递推关系的应用、“累加求和”、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
16.在区间[0,1]上随机取两个数x,y,记P为事件“x+y≤$\frac{2}{3}$”的概率,则P=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{9}$ |
17.关于x的不等式x2-4x+5<a2-2a-2的解集不是空集,则实数a的取值范围是( )
| A. | (-∞,-1)∪(3,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | (-1,3) | D. | [-1,3] |
19.若复数z满足(1-i)z=i,则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
 定义:如果两个椭圆的离心率相等,那么称这两个椭圆相似,它们的长轴长之比(大于1)叫做这两个椭圆的相似比.(1)设m,n∈N*,试判断椭圆C1:$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{m}$=1和椭圆C2:$\frac{{x}^{2}}{m+n}$+$\frac{{y}^{2}}{m+1}$=1能否相似?若能,求出它们的相似比;若不能,请说明理由.
定义:如果两个椭圆的离心率相等,那么称这两个椭圆相似,它们的长轴长之比(大于1)叫做这两个椭圆的相似比.(1)设m,n∈N*,试判断椭圆C1:$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{m}$=1和椭圆C2:$\frac{{x}^{2}}{m+n}$+$\frac{{y}^{2}}{m+1}$=1能否相似?若能,求出它们的相似比;若不能,请说明理由.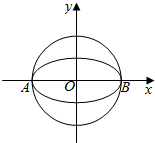 已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.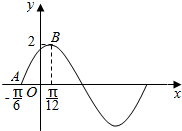 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示