题目内容
18.已知函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$(x∈R).(1)判断函数f(x)的奇偶性;
(2)用定义判断函数f(x)的单调性;
(3)解不等式f(1-m)+f(1-m2)<0.
分析 (1)利用函数奇偶性求解即可,对于奇偶性的判断,只须考虑f(-x)与f(x)的关系即得;
(2)单调性的定义对于单调性的证明,先在定义域中任取两个实数x1,x2,且x1<x2,再比较f(x1)-f(x2)即可;
(3)先依据函数y=f(x)在R上单调性化掉符号:“f”,将问题转化为关于m的整式不等式,再利用一元二次不等式的解法即可求得m的取值范围
解答 解:(1)∵f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-f(x),∴函数f(x)为奇函数,
(2)证明:f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$=1-$\frac{2}{{2}^{x}+1}$
在定义域中任取两个实数x1,x2,且x1<x2,
则f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$.
∵x1<x2,∴0<${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,从而f(x1)-f(x2)<0
∴函数f(x)在R上为单调增函数.
(3)由(2)得函数f(x)为奇函数,在R上为单调增函数,
∴f(1-m)+f(1-m2)<0即f(1-m)<-f(1-m2),
∴f(1-m)<f(m2-1),1-m<m2-1
∴原不等式的解集为(-∞,-2)∪(1,+∞)
点评 本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法、函数的值域等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.一个几何体的三视图如图所示,则该几何体的表面积为( )
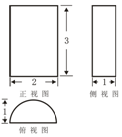

| A. | 4π | B. | 5π+6 | C. | 3π+6 | D. | 4π+6 |
 如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.
如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.