题目内容
已知tanα=
,tan(β-α)=-
,则tanβ= .
| 1 |
| 2 |
| 1 |
| 3 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:直接利用两角和的正切函数求解即可.
解答:
解:∵tanα=
tan(β-α)=-
,
∴
=-
,
可得
=-
,
解得tanβ=
.
故答案为:
;
| 1 |
| 2 |
tan(β-α)=-
| 1 |
| 3 |
∴
| tanβ-tanα |
| 1+tanαtanβ |
| 1 |
| 3 |
可得
tanβ-
| ||
1+
|
| 1 |
| 3 |
解得tanβ=
| 1 |
| 7 |
故答案为:
| 1 |
| 7 |
点评:本题考查两角和的正切函数的应用,考查计算能力.

练习册系列答案
相关题目
已知函数f(x)=2
cosxsin(x+
)-1(x∈R).则函数f(x)在区间[-
,
]上的最大值和最小值分别是( )
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
A、最大值为
| ||||
B、最大值为
| ||||
C、最大值为2
| ||||
| D、最大值为1,最小值为-1 |
在△ABC中,tan
=2sinC,若AB=1,求△ABC周长的取值范围( )
| A+B |
| 2 |
| A、(2,3] |
| B、[1,3] |
| C、(0,2] |
| D、(2,5] |
下列各式(等式或不等式)中,不成立的是( )
A、(
| ||||||
| B、log67>log76 | ||||||
| C、lg15=1+lg3-lg2 | ||||||
| D、log49=2log23 |
 如图,某农场要修建3个养鱼塘,每个面积为10000米2,鱼塘前面要留4米的运料通道,其余各边为2米宽的堤埂,则占地面积最少时,每个鱼塘的长、宽分别为( )
如图,某农场要修建3个养鱼塘,每个面积为10000米2,鱼塘前面要留4米的运料通道,其余各边为2米宽的堤埂,则占地面积最少时,每个鱼塘的长、宽分别为( )A、长102米,宽
| ||
| B、长150米,宽66米 | ||
| C、长、宽均为100米 | ||
D、长150米,宽
|
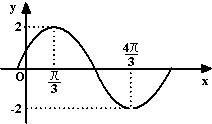 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<