题目内容
10.函数f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$的最小正周期为2π.分析 利用同角三角函数基本关系式化简函数解析式可得f(x)=$\frac{|sinx|}{cosx}$,又y=|sinx|的周期为π,cosx的周期为2π,结合函数的图象化简求得其周期.
解答 解:∵f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$=$\frac{|sinx|}{cosx}$,又y=|sinx|的周期为π,cosx的周期为2π,
作出其图象如下: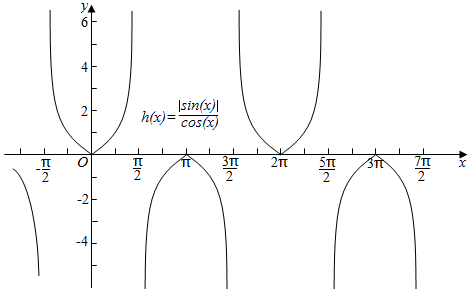
∴可得函数f(x)=$\frac{\sqrt{1-co{s}^{2}x}}{cosx}$=$\frac{|sinx|}{cosx}$的最小正周期为2π.
故答案为:2π.
点评 本题主要考查三角函数的周期性及其求法,利用了y=Asin(ωx+φ )、y=Asin(ωx+φ )的周期等于$\frac{2π}{ω}$,y=|Asin(ωx+φ )|、y=|Asin(ωx+φ )|的周期等于$\frac{π}{ω}$,属于基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
19.若方程$\frac{{x}^{2}}{3-m}$+$\frac{{y}^{2}}{m-1}$=1表示焦点在y轴上的椭圆,则实数m的取值范围为( )
| A. | (-∞,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |