题目内容
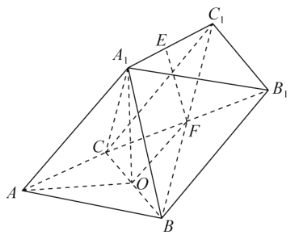
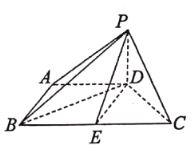
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据线面垂直的判定定理,证明
,根据线面垂直的判定定理,证明![]() 平面
平面![]() ,进而可得线线垂直;
,进而可得线线垂直;
(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,根据题中条件,分别求出两平面的法向量,求出两向量夹角的余弦值,即可得出结果.
,根据题中条件,分别求出两平面的法向量,求出两向量夹角的余弦值,即可得出结果.
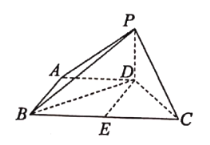
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以四边形
,所以四边形![]() 是平行四边形.
是平行四边形.
因为![]() 所以四边形
所以四边形![]() 是矩形.
是矩形.
所以![]() .
.
又![]()
所以![]() .
.
所以![]() 是直角三角形,即
是直角三角形,即![]() .
.
又![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() .
.
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)如图,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
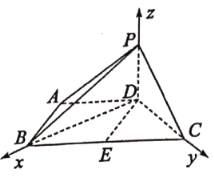
设![]() ,则
,则![]() ,
,
由(1)知![]() ,
,![]() ,
,![]() .
.
![]() ,
,
所以![]() .
.
所以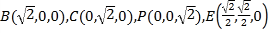
所以![]()
![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则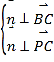
所以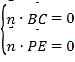 ,即
,即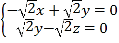 ,
,
取![]() ,则
,则![]() ,
,![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
又平面![]() 的一个法向量为
的一个法向量为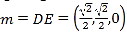
所以![]()
所以平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值为
所成的角(锐角)的余弦值为![]() .
.

【题目】某公司生产某种产品,一条流水线年产量为![]() 件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
件,该生产线分为两段,流水线第一段生产的半成品的质量指标会影响第二段生产成品的等级,具体见下表:
第一段生产的半成品质量指标 |
|
|
|
第二段生产的成品为一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生产的成品为二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生产的成品为三等品概率 | 0.5 | 0.3 | 0.1 |
从第一道生产工序抽样调查了![]() 件,得到频率分布直方图如图:
件,得到频率分布直方图如图:

若生产一件一等品、二等品、三等品的利润分别是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各组的中间值估计为该组半成品的质量指标,估算流水线第一段生产的半成品质量指标的平均值;
(Ⅱ)将频率估计为概率,试估算一条流水线一年能为该公司创造的利润;
(Ⅲ)现在市面上有一种设备可以安装到流水线第一段,价格是![]() 万元,使用寿命是
万元,使用寿命是![]() 年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布
年,安装这种设备后,流水线第一段半成品的质量指标服从正态分布![]() ,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
,且不影响产量.请你帮该公司作出决策,是否要购买该设备?说明理由.
(参考数据:![]() ,
,![]() ,
,![]() )
)