题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 与椭圆
与椭圆![]() 只有一个公共点的直线为
只有一个公共点的直线为![]() ,过点
,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求证:
,求证:![]() 与
与![]() 的交点在定直线上,并求出该定直线的方程.
的交点在定直线上,并求出该定直线的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析,
;(Ⅱ)证明见解析,![]() ,
,
【解析】
(Ⅰ)设![]() ,
,![]() ,根据点
,根据点![]() ,
,![]() 都在椭圆上,代入椭圆方程两式相减,根据“设而不求”的思想,结合离心率以及中点坐标公式、直线的斜率建立等式即可求解.
都在椭圆上,代入椭圆方程两式相减,根据“设而不求”的思想,结合离心率以及中点坐标公式、直线的斜率建立等式即可求解.
(Ⅱ)设![]() ,由对称性,设
,由对称性,设![]() ,由
,由![]() ,得椭圆上半部分的方程为
,得椭圆上半部分的方程为![]() ,从而求出直线
,从而求出直线![]() 的方程,再由过点
的方程,再由过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求出
,求出![]() ,两方程联立,消去
,两方程联立,消去![]() ,即可求解.
,即可求解.
(Ⅰ)由题可知![]() ,直线
,直线![]() 的斜率存在.
的斜率存在.
设![]() ,
,![]() ,由于点
,由于点![]() ,
,![]() 都在椭圆上,
都在椭圆上,
所以![]() ①,
①,![]() ②,
②,
①-②,化简得![]() ③
③
又因为离心率为![]() ,所以
,所以![]() .
.
又因为直线![]() 过焦点
过焦点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,
所以![]() ,
,![]() ,
,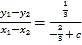 ,
,
代入③式,得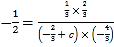 ,解得
,解得![]() .
.
再结合![]() ,解得
,解得![]() ,
,![]() ,
,
故所求椭圆的方程为![]() .
.
(Ⅱ)证明:设![]() ,由对称性,设
,由对称性,设![]() ,由
,由![]() ,得椭圆上半部分的方程为
,得椭圆上半部分的方程为![]() ,
,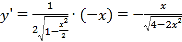 ,
,
又![]() 过点
过点![]() 且与椭圆只有一个公共点,所以
且与椭圆只有一个公共点,所以![]() ,
,
所以![]() :
:![]() ,④
,④
因为![]() 过点
过点![]() 且与
且与![]() 垂直,所以
垂直,所以![]() :
:![]() ,⑤
,⑤
联立④⑤,消去![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,从而可得
,从而可得![]() ,
,
所以![]() 与
与![]() 的交点在定直线
的交点在定直线![]() 上.
上.

 黄冈天天练口算题卡系列答案
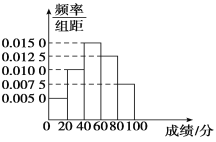
黄冈天天练口算题卡系列答案【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: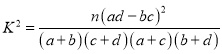 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |