题目内容
14.已知某几何体的一条棱长为a,在正视图中的投影长为2$\sqrt{3}$,在侧视图,俯视图中投影长分别为m、n,且m+n=6,则a的最小值为4.分析 作出线段在空间坐标系中的投影和直观图,利用勾股定理求出m,n.则a的最小值为n.
解答 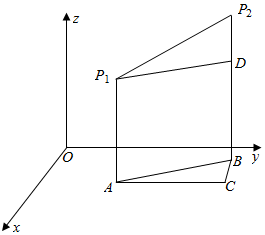 解:作出空间坐标系如图,设几何体的棱为P1P2,作出它在平面xoy上的投影AB,
解:作出空间坐标系如图,设几何体的棱为P1P2,作出它在平面xoy上的投影AB,
过A作AC∥y轴,过B作BC∥x轴,交点为C,则AC=2$\sqrt{3}$,BC=m,AB=n.
由勾股定理得(2$\sqrt{3}$)2+m2=n2,又∵m+n=6,∴n=4,m=2.
过P1作P1D⊥P2B,则P1D=AB=4.P2D为P1P2的竖坐标之差.
∴P1P2=$\sqrt{{P}_{1}{D}^{2}+{P}_{2}{D}^{2}}$=$\sqrt{16+{P}_{2}{D}^{2}}$.
∴当P2D=0时,P1P2取得最小值4.
故答案为:4.
点评 本题考查了物体的三视图,找到m,n的关系求出m,n是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
1.已知函数f(x)=2x+2x-6的零点为x0,那么x0所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
2.已知a>0且a≠1,下列函数中,在区间(0,a)上一定是减函数的是( )
| A. | f(x)=$\frac{2x-a}{x}$ | B. | f(x)=ax | C. | f(x)=loga(ax) | D. | f(x)=x2-3ax+1 |