题目内容
已知 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)直接写出 的单调区间(不需给出演算步骤);
的单调区间(不需给出演算步骤);
(Ⅲ)求不等式 解集.
解集.
(Ⅰ) ;(Ⅱ)递增区间:
;(Ⅱ)递增区间: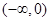 ,
,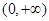 ;
;
(Ⅲ):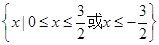 。
。
解析试题分析:(Ⅰ)当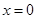 时,
时,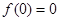 ;
;
当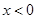 时,则
时,则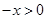 ,
,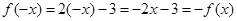 ,则
,则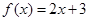
综上: 7分
7分
(Ⅱ)递增区间: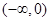 ,
,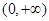 10分
10分
(Ⅲ)当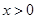 时,
时, ,即
,即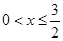
当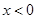 时,
时,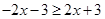 ,即
,即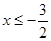
当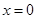 时,
时,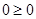 ,恒成立
,恒成立
综上,所求解集为: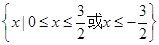 15分
15分
考点:本题主要考查分段函数的概念,函数的奇偶性、单调性,简单不等式组的解法。
点评:典型题,高一阶段,此类题目较为典型,利用分段函数的奇偶性,确定函数的解析式。解涉及分段函数不等式求解问题,必须注意分段讨论。

练习册系列答案
相关题目
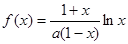 .
.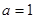 ,讨论
,讨论 的单调性;
的单调性; ,
,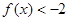 ,求实数
,求实数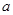 的取值范围.
的取值范围.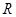 上的函数
上的函数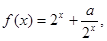
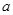 为常数,若
为常数,若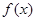 为偶函数,
为偶函数,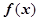 在
在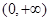 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明; .
.  的奇偶性;
的奇偶性; ,求
,求 的值.
的值.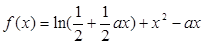
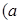 为常数,
为常数,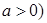
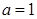 时,求函数
时,求函数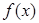 在
在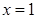 处的切线方程;
处的切线方程; 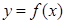 在
在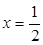 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程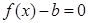 在
在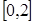 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数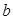 的取值范围;
的取值范围;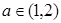 ,总存在
,总存在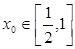 ,使不等式
,使不等式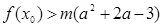 成立,求实数
成立,求实数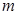 的取值范围。
的取值范围。 (
(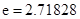 …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为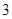 .
. 的值;
的值;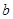
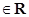 且
且 ,试解关于
,试解关于 的不等式
的不等式 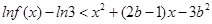 ;
;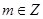 且
且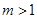 .若存在实数
.若存在实数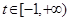 ,使得对任意的
,使得对任意的 ,都有
,都有 ,试求
,试求 的最大值.
的最大值. 求
求
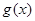 分别由下表给出:
分别由下表给出:
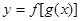 ,并画出函数
,并画出函数 ,其中
,其中 ,且a≠0.
,且a≠0. 在区间[1,e]上的最小值;
在区间[1,e]上的最小值; 的偶函数
的偶函数 .
.  的值;
的值;  的单调性;
的单调性; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.