题目内容
已知函数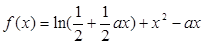
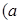 为常数,
为常数,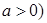
(1)当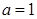 时,求函数
时,求函数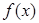 在
在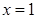 处的切线方程;
处的切线方程;
(2)当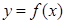 在
在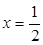 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程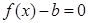 在
在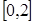 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数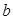 的取值范围;
的取值范围;
(3)若对任意的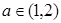 ,总存在
,总存在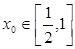 ,使不等式
,使不等式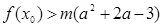 成立,求实数
成立,求实数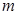 的取值范围。
的取值范围。
(1) 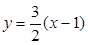 (2)
(2) 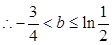
(3) 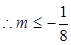
解析试题分析:(1)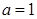 时,
时,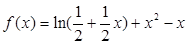
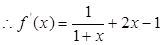 ,于是
,于是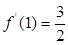 ,又
,又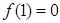 ,即切点为(
,即切点为(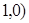
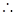 切线方程为
切线方程为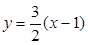 —————————————————————————5分
—————————————————————————5分
(2)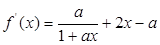 ,
,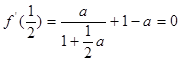 ,即
,即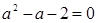 ,
,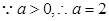
此时,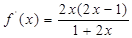 ,
,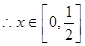 上减,
上减,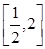 上增,
上增,
又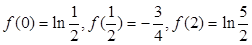
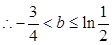 ———————————————————————————10分
———————————————————————————10分
(3)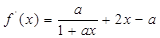
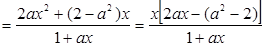
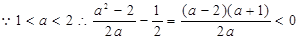 ,即
,即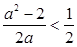 (
(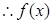 在
在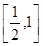 上增,
上增,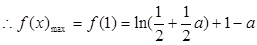
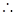 只须
只须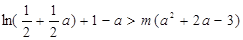 ————————————————12分
————————————————12分
(法一)设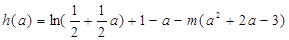
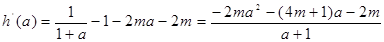
又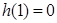
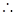
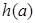 在1的右侧需先增,
在1的右侧需先增,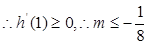
设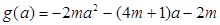 ,对称轴
,对称轴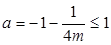
又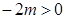 ,
,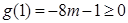
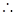 在
在 上,
上,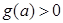 ,即
,即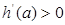
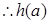 在
在 上单调递增,
上单调递增,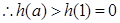
即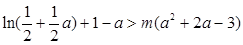 ,
,
于是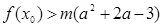
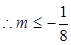 ——————————————————-15分
——————————————————-15分
(法二)
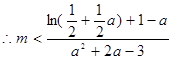
设
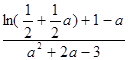 ,
,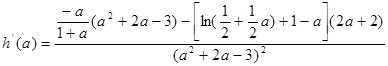
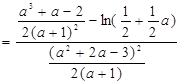
设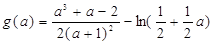 ,
,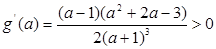
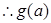 在
在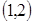 上增,又
上增,又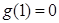 ,
,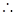
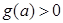 ,即
,即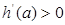 ,
,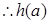 在
在 上增
上增
又
数学 选修1B模块答案
题号:03答案
(1)法一:由柯西不等式知: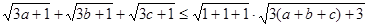
 ——————————————————5分
——————————————————5分
法二: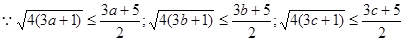
相加得: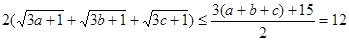
 ——————————————————————5分
——————————————————————5分
法三:令
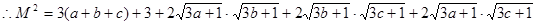
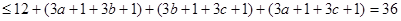
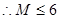

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 上的函数
上的函数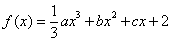 同时满足以下条件:
同时满足以下条件: 在
在 上是减函数,在
上是减函数,在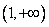 上是增函数;②
上是增函数;②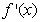 是偶函数;
是偶函数; 处的切线与直线
处的切线与直线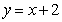 垂直.
垂直.  的解析式;
的解析式;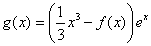 ,求函数
,求函数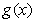 在
在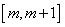 上的最小值.
上的最小值.
 时,求
时,求 的单调区间;
的单调区间; ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.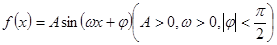 在一个周期内的部分函数图象如图所示,(I)求函数
在一个周期内的部分函数图象如图所示,(I)求函数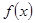 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数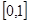 上的最大值和最小值.
上的最大值和最小值.
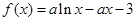 (a∈R且
(a∈R且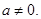 ).
). 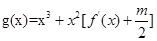 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围. 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
. 解集.
解集.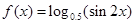
 令
令 .
. 的表达式;
的表达式; 和函数
和函数 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围. .
.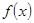 在
在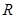 上为增函数;
上为增函数; 的值;
的值; 上的值域.
上的值域.