题目内容
设
为三角形
的三边，求证：
证明：要证明： 
需证明：a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)
需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c
∵a,b,c是
的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
∴a+2ab+b+abc>c ∴
成立。
练习册系列答案
名校课堂系列答案
相关题目
.某班甲、乙两名学同参加100米达标训练，在相同条件下两人10次训练的成绩(单位：秒)如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 甲 | 11.6 | 12.2 | 13.2 | 13.9 | 14.0 | 11.5 | 13.1 | 14.5 | 11.7 | 14.3 |
| 乙 | 12.3 | 13.3 | 14.3 | 11.7 | 12.0 | 12.8 | 13.2 | 13.8 | 14.1 | 12.5 |
(1)从甲、乙两人的10次训练成绩中各随机抽取一次，求抽取的成绩中至少有一个比12.8秒差的概率．
(2)后来经过对甲、乙两位同学的多次成绩的统计，甲、乙的成绩都均匀分布在[11.5,14.5 ]之间，现甲、乙比赛一次，求甲、乙成绩之差的绝对值小于0.8秒的概率．
≥2，x＋
＝
＋
≥n＋1 (n∈N*)，则m＝______
，则
，则
＝ ．
满足
（
是虚数单位），则
的最小值为 ．
中，已知
，则该三角形的形状为 ．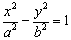
（
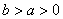）的左、右焦点分别为 F1，F2．若在双曲线的右支上存在
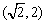D．