Question

.某班甲、乙两名学同参加100米达标训练，在相同条件下两人10次训练的成绩(单位：秒)如下：

	1	2	3	4	5	6	7	8	9	10
甲	11.6	12.2	13.2	13.9	14.0	11.5	13.1	14.5	11.7	14.3
乙	12.3	13.3	14.3	11.7	12.0	12.8	13.2	13.8	14.1	12.5

 (1)从甲、乙两人的10次训练成绩中各随机抽取一次，求抽取的成绩中至少有一个比12.8秒差的概率．

(2)后来经过对甲、乙两位同学的多次成绩的统计，甲、乙的成绩都均匀分布在[11.5,14.5 ]之间，现甲、乙比赛一次，求甲、乙成绩之差的绝对值小于0.8秒的概率．

Answer 1

解　(1)设事件A为：甲的成绩低于12.8，事件B为：乙的成绩低于12.8，

则甲、乙两人成绩至少有一个低于12.8秒的概率为

P＝1－P(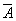)()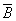＝1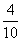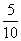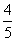－×＝.              ………………5分

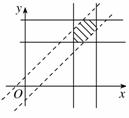
(2)设甲同学的成绩为x，乙同学的成绩为y，

则|x－y|<0.8，  得－0.8＋x<y<0.8＋x.                         

如图阴影部分面积即为3×3－2.2×2.2＝4.16，      ………………9分

则P(|x－y|<0.8)＝P(－0.8＋x<y<0.8＋x)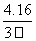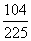＝＝.…………12分