题目内容
已知圆x2+y2=1,过点A(1,0)作直线交圆于Q,在直线上取一点P,使P到x=-1的距离等于|PQ|,求点P的轨迹方程.
考点:轨迹方程
专题:综合题,直线与圆
分析:设P(x,y),过P作圆的切线PB,则|PB|2=x2+y2-1,曲圆幂定理得(x+1)2[(x-1)2+y2]=(x2+y2-1)2
展开整理,得出结论.
展开整理,得出结论.
解答:
解:设P(x,y),过P作圆的切线PB,则|PB|2=x2+y2-1,
由已知条件,知|PQ|=|x-1|,|PA|=
.
曲圆幂定理得(x+1)2[(x-1)2+y2]=(x2+y2-1)2
展开整理,得y2(x2+y2-2x-3)=0,
可见,所求轨迹由x轴与一个圆组成.此圆的圆心为A(1,0)半径为2.
即y=0和x2+y2-2x-3=0.
由已知条件,知|PQ|=|x-1|,|PA|=
| (x-1)2+y2 |
曲圆幂定理得(x+1)2[(x-1)2+y2]=(x2+y2-1)2
展开整理,得y2(x2+y2-2x-3)=0,
可见,所求轨迹由x轴与一个圆组成.此圆的圆心为A(1,0)半径为2.
即y=0和x2+y2-2x-3=0.
点评:本题是中档题,考查轨迹方程的求法,利用转化思想是本题解答的关键,考查计算能力,逻辑推理能力,常考题型.

练习册系列答案
相关题目
集合M={x|x>0},集合N={x|1-x>0},则M∩N等于( )
| A、(0,1) |
| B、(-∞,0) |
| C、(-∞,-1) |
| D、(-∞,1) |
为了得到y=cos(2x+
)函数的图象,只需将余弦函数曲线上所有的点( )
| 1 |
| 3 |
A、先向右平移
| ||||
B、先向左平移
| ||||
C、先向左平移
| ||||
D、先向右平移
|
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知bcosB=acosA,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
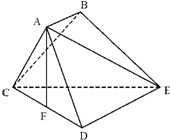 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.