题目内容
5.设函数f(x)=(sinx+cosx)2-$\sqrt{3}$cos2x.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在[0,$\frac{π}{2}$]上的最大值,以及取得最大值时对应x的值.
分析 (Ⅰ)化函数f(x)为正弦型函数,根据T=$\frac{2π}{ω}$求出f(x)的最小正周期;
(Ⅱ)可求x∈[0,$\frac{π}{2}$]时sin(2x-$\frac{π}{3}$)的取值范围,求出x=$\frac{5π}{12}$时f(x)取得最大值.
解答 解:(Ⅰ)函数f(x)=(sinx+cosx)2-$\sqrt{3}$cos2x
=sin2x+2sinxcosx+cos2x-$\sqrt{3}$cos2x
=sin2x-$\sqrt{3}$cos2x+1
=2sin(2x-$\frac{π}{3}$)+1,
∴f(x)的最小正周期为T=$\frac{2π}{2}$=π;
(Ⅱ)当x∈[0,$\frac{π}{2}$]时,
2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
sin(2x-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1];
∴当x=$\frac{5π}{12}$时,f(x)=2sin(2×$\frac{5π}{12}$-$\frac{π}{3}$)+1=3取得最大值.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题目.

| A. | $\frac{25}{18}$ | B. | $-\frac{25}{18}$ | C. | $\frac{7}{18}$ | D. | $-\frac{7}{18}$ |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
商丘市某高中从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100),4.
(Ⅰ)请把给出的样本频率分布表中的空格都填上;
(Ⅱ)估计成绩在85分以上学生的比例;
(Ⅲ)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100)中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | 0.30 |
[80,90) | ||
[90,100) | 4 | 0.08 |
合计 |
 的前
的前 项和为
项和为 ,已知
,已知 ,求
,求 和
和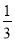 ,P(N)=
,P(N)=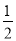
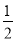 ,P(N)=
,P(N)=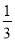 ,P(N)=
,P(N)=