题目内容
6.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,其余人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,其余人主要的休闲方式是运动.(1)根据以上数据建立一个2×2的列联表;
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | ||
| 女性 | 43 | 70 | |
| 合计 | 124 |
参考临界值表
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
分析 (1)由已知数据即可得出表格.
(2)利用k2计算公式得出,通过比较临界值表即可得出.
解答 解:(1)
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | 33 | 54 |
| 女性 | 43 | 27 | 70 |
| 合计 | 64 | 60 | 124 |
所以不能在犯错误的概率不超过0.01的前提下认为休闲方式与性别有关系.
点评 本题考查了独立性检验原理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.若直线y=x+t与椭圆$\frac{x^2}{4}+{y^2}=1$相交于A,B两点,当|t|变化时,|AB|的最大值为( )
| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{4\sqrt{10}}}{5}$ | D. | $\frac{{8\sqrt{10}}}{5}$ |
11.某调查机构为了研究“户外活动的时间长短”与“患感冒”两个分类变量是否相关,在该地随机抽取了若干名居民进行调查,得到数据如表所示:
若从被调查的居民中随机抽取1人,则取到活动时间超过1小时的居民的概率为$\frac{3}{5}$.
(1)完善上述2×2列联表;
(2)能否在犯错误的概率不超过0.1%的前提下,认为“户外活动的时间长短”与“患感冒”两者间相关.
| 患感冒 | 不患感冒 | 合计 | |
| 活动时间超过1小时 | 20 | 40 | 60 |
| 活动时间低于1小时 | 30 | 10 | 40 |
| 合计 | 50 | 50 | 100 |
(1)完善上述2×2列联表;
(2)能否在犯错误的概率不超过0.1%的前提下,认为“户外活动的时间长短”与“患感冒”两者间相关.
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
15.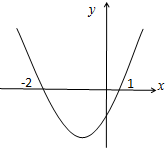 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
 若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2),无极小值 | B. | 函数f(x)有极大值f(1),无极小值 | ||
| C. | 函数f(x)有极大值f(-2)和极小值f(1) | D. | 函数f(x)有极大值f(1)和极小值f(-2). |
16.已知圆(x-1)2+(y-1)2=4上到直线y=x+b的距离等于1的点有且仅有2个,则b的取值范围是( )
| A. | (-$\sqrt{2}$,0)U(0,$\sqrt{2}$) | B. | (-3$\sqrt{2}$,3$\sqrt{2}$) | C. | (-3$\sqrt{2}$,-$\sqrt{2}$)U($\sqrt{2}$,3$\sqrt{2}$) | D. | (-3$\sqrt{2}$,-$\sqrt{2}$]U($\sqrt{2}$,3$\sqrt{2}$) |